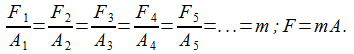
TWENTIETH CENTURY LIBRARY
HIRAM HAYDN, EDITOR
Published:
HENRI POINCARÉ by Tobias Dantzig
THORSTEIN VEBLEN by David Riesman
FRANZ BOAS by Melville J. Herskovits
MAHATMA GANDHI by Haridas T. Muzumdar
SIGMUND FREUD by Gregory Zilboorg
JOHN DEWEY by Jerome Nathanson
OSWALD SPENGLER by H. Stuart Hughes
JAMES JOYCE by W. Y. Tindall
CHARLES DARWIN by Paul B. Sears
ALBERT EINSTEIN by Leopold Infeld
GEORGE BERNARD SHAW by Edmund Fuller
FYODOR DOSTOEVSKY by Rene Fueloep-Miller
WILLIAM JAMES by Lloyd Morris
♦
In Preparation:
JOHN MAYNARD KEYNES by Seymour Harris
KARL MARX by Max Lerner
ALFRED NORTH WHITEHEAD by Stanley Newburger
FRIEDRICH NIETZSCHE by James Gutmann
CHARLES SCRIBNER'S SONS
Henri Poincaré
COPYRIGHT, 1954,
BY TOBIAS DANTZIG
Printed in the United States of America
All rights reserved. No part of this book
may be reproduced in any form
without
the permission of Charles Scribner's Sons
A
Library of Congress Catalog Card No. 54-7250
I AM indebted to Mrs. Alice Gazin for her conscientious assistance in the preparation of the manuscript of the present volume; to Professor M. A. Greenfield of the University of California at Los Angeles for editorial assistance; last, but not least, to Mr. Charles Scribner whose critical comments led to the clarification of several difficult points in the exposition.
Tobias Dantzig
THE crisis in the foundations of the exact sciences, which had begun during Poincaré's lifetime, did not reach a climax till decades after his death. His analysis of the issues of his time foreshadowed the trend; but, deep as was his insight and broad as was his horizon, even he could not have foreseen the extent and ramifications of the imminent upheaval. No more, for that matter, than a political observer of his time, however keen, could have predicted the World Wars and the social and economic upheavals which followed in their wakes.
This circumstance posed a serious dilemma to the writer of the present book. Should he confine the work to an analysis of Poincaré's scientific philosophy, as reflected in the writings of the great thinker, studiously avoiding comments on the epochmaking events which took place after his death? Or should he present his own reactions to those events and to the issues raised by these events as corollaries to Poincaré's philosophy, supporting these arrogations by specious quotations from chapter and verse? It was the odious choice between writing a worthless epitaph on the tomb of a prophet and a spurious claim of a pretender that the mantle of the prophet had fallen on his shoulders.
After much deliberation the author found a third course open to him. The essays here assembled are not intended as chapters of a systematic exposition of the scientific philosophy of Poincaré. They are—to use a musical idiom—at best, VARIATIONS ON THEMES OF POINCARÉ. This writer does not pretend that he has interpreted the contemporary issues of science as Poincaré would have seen these issues, had he lived to see them. He does believe, however, that he has interpreted these issues in the light of the teachings of the great thinker, as it was given to this writer to see that light.
In preparing this book, the writer leaned heavily on an [Pg x]earlier work which is now out of print and circulation. The preface to the French edition of that work contains the following passage: "To me the French edition of my work is not a mere translation, but a transcription of ideas into a language in which it should have been written in the first place, the language in which thought and taught one, whom I proudly acknowledge as my master. His words are among the most brilliant recollections of my youth; his piercing wisdom and potent prose have inspired my efforts of a riper age. To the memory of Henri Poincaré, the intellectual giant who was the first to recognize the role which the idiosyncrasies of the race play in the evolution of scientific ideas, I dedicate this book."
Sic sentio, sic volo!
TOBIAS DANTZIG
Pacific Palisades, California
December 25, 1953
| ACKNOWLEDGMENTS | ||
| PREFACE | ||
| CHAPTER | I. | THE ICONOCLAST |
| CHAPTER | II. | THE AGE OF INNOCENCE |
| CHAPTER | III. | THE MECHANISTIC CONQUEST |
| CHAPTER | IV. | IN QUEST OF THE ABSOLUTE |
| CHAPTER | V. | EUCLIDES VINDICATUS |
| CHAPTER | VI. | TEMPLETS |
| CHAPTER | VII. | ON RIGID STANDARDS |
| CHAPTER | VIII. | ON RHYTHM AND DURATION |
| CHAPTER | IX. | ON CLOCKS AND SIGNALS |
| CHAPTER | X. | STRAIGHT AND STEADY |
| CHAPTER | XI. | THE COSMIC WEB |
| CHAPTER | XII. | FIGURES DO NOT LIE |
| CHAPTER | XIII. | A UNIVERSE OF DISCOURSE |
| CHAPTER | XIV. | THE INFINITE |
| CHAPTER | XV. | INDUCTION AND INFERENCE |
| CHAPTER | XVI. | SCIENCE AND REALITY |
| LIFE AND WORK | ||
| SELECTIVE INDEX |
Only Science and Art make civilization worth-while. One may be startled by the formula: Science for the sake of Science; and yet, it is worth as much as Life for Life's sake, if life is but misery; and even as Happiness for Happiness' sake, unless one believes that all pleasures are the same in quality, unless one is ready to admit that the goal of civilization is to furnish alcohol to all who love to drink.
All actions have goals. We must suffer, we must work, we must pay for our seats at the show. But, we pay that we may see, or that, at least, others may see some day.
Henri Poincaré, The Value of Science
SURVEYING what has been written on the life, opinions, interests, character, moods and idiosyncrasies of Henri Poincaré, one is overcome by the abundance of material and, at the same time, bewildered by the discordance of the accounts. A few incontrovertible facts and authenticated data; a host of rumors and conjectures, some plausible, some specious, some spurious, some absurd. This confusion is inevitable: a man who is an international celebrity at the age of 35 is bound to become a legend by 58. To use such material for an authentic portrait is difficult enough. But there is an even greater difficulty: to describe means to classify, and the man Poincaré defies classification, as does indeed his philosophy.
Let us begin with some vital statistics [P]. He came from a prosperous middle-class family [P]. The etymology of the name is uncertain, the most plausible conjecture being that it originally read Poing-Carré, i.e., Square Fist. He was a native of Nancy, as was his father, Leon, and his uncle Antoine, the father of Raymond Poincaré [P], president of France from 1913 to 1920.
[Pg 2]Henri Poincaré was born on the 29th of April, 1854. He received his secondary education in the Lycée of Nancy and graduated at the age of 17. He entered the École Polytechnique at the age of 19. He resided for the greater part of his mature life in Paris, where he died on July 17, 1912, after a "successful" operation on the prostate. He married the great-granddaughter of the famous naturalist Geoffroi-Saint-Hilaire and had by her four children.
At the age of five, he suffered a set-back, when a severe case of diphtheria, followed by a paralysis of the larynx, kept him speechless for nine months. He recovered his voice, but not his physical strength. The prolonged sickness left him frail and tender, and this weakness, in turn, prevented him from taking part in exercises and games, where strength, physical skill or endurance were required.
I saw him often between the years 1906 and 1910, when I was a student at the Sorbonne. I recall above all his unusual eyes: myopic, yet luminous and penetrating. Otherwise, my memory is that of a man small in stature, stooped and ill at ease, as it were, in limb and joint. This last impression was accentuated by his manner of writing on the blackboard. For, his penmanship was very bad, and his draftsmanship even worse. He was ambidextrous, and I recall an ironical remark of a fellow-student to the effect that Poincaré could use either hand with equal ease and dexterity.
The circles he drew on the board were purely formal, resembling the normal variety only in that they were closed and convex. This manual deficiency was responsible for a "detour" in the career of Poincaré. The story is worth telling. After leading his class at the École Polytechnique, Poincaré lost his first place by failing the final examination in Descriptive Geometry [G]. It appears that the test problem was to determine graphically the oblique section of a circular cone. Unable or unwilling to carry out the mechanical drawing in detail, Poincaré calculated the curve by means of analytical geometry and presented his result without recording the intermediary steps. To the examiner this omission of detail was bad enough; but this was not the only [Pg 3]sin of the examinee: Poincaré's ellipse had the correct dimensions, but not the correct orientation!
A formal biography of Poincaré would read like a catalogue of academic honors: from degree to degree, from title to title, from grand prize to grand prize. Titular professor at the Sorbonne at 30, member of the Institute at 32; all the homage which his native land could grant was bestowed upon him before he turned 40. And not only his native land: universities and learned societies on both sides of the Atlantic showered him with prizes, medals and honorary degrees.
Congresses and conventions, jubilees and festivals vied with each other for his presence, and Poincaré passionately loved to travel. His travelogue would comprise practically every country in Europe and the United States, which, incidentally, he visited at least twice. An estimate of the time consumed in this journeying leaves one aghast. When did this extraordinary man find time to present more than 500 memoirs, publish 30 odd treatises, write scores of tracts on the foundations of science? Yet, he did all this, and more: for, he was active on many scientific commissions, and pronounced scores of eloquent eulogies in memory of illustrious scholars of his time.
These eulogies were not restricted to French savants. And this brings me to an aspect of Poincaré's character that I, for one, can not quite fathom: I am speaking of his attitude towards his German contemporaries.
Poincaré was 16, when the Franco-German war [F] broke out. Nancy was on the direct line of the Prussian advance, and wounded French by the hundreds were being brought to the city. His father was one of the physicians in charge of caring for these wounded, and Henri acted as his ambulance assistant. Thus he got a first-hand acquaintance with the misery inflicted by the ruthless invader. He also saw the estate of his maternal grandfather laid waste, the Prussians carrying off what they could and wantonly destroying what they could not carry. He saw his native city occupied and treated with all the arrogance a Prussian overlord could muster. The Germans evacuated France in [Pg 4]1873, but the tension continued for many years to come, the Bismarck-inspired papers agitating for a new war [F] to crush France before it had a chance to recover, while the French patriots, smarting under the humiliating defeat, clamored for La Revanche.
Yes, there was much grist for rancor to feed on. So, let us look at the record. During the occupation Poincaré taught himself to read German. In fact, he learned the language so well that he could read German newspapers fluently: in this way he managed to stay abreast of events and to brief his friends during the period when French journals were banned. In the years to come he kept up his German studies, and it may be said without exaggeration that no Frenchman had a better knowledge of German mathematical and physical literature than Poincaré. And this takes me to the first episode of this queer story.
One of the earliest mathematical achievements of Poincaré was a generalization of the so-called elliptic functions. He could have called these functions ultra-elliptic, or pan-elliptic: he chose instead to call them Fuchsian, in honor of the German, Fuchs, who had indicated their possibility without proving their existence. This homage must have raised many a French eyebrow, as evidenced by an epigram which I heard twenty years later. This would read in free translation: "The only Fuchsian claim to fame is that a French discovery bears his name." These protests did not disturb Poincaré: for, a few months later he presented the French Academy of Sciences with a new discovery which he called Kleinean Groups, honoring the German mathematician, Felix Klein [K]. There were several similar incidents where, it seemed, Poincaré had been leaning backwards to pay homage to German scientists: the most striking of all occurred at Göttingen in 1909, when Poincaré delivered a series of six lectures, five of these in German!
Nor was this generosity confined to German scientists: the English, Italian and Russian came in for their shares. The latter were not any more popular in France than the Germans, and I recall that Poincaré's frequent references to Lobachevsky [L] led one French writer to brand non-Euclidean geometry [G] as "Geometrical Nihilism of Slav Origin."
[Pg 5]I do not presume to know the motives back of Poincaré's behavior towards foreign scientists, but there is no doubt that this attitude paved the way to that cosmopolitanism in science which has survived two hot wars, and bids fair to survive the cold war which is now upon us.
We come to the year 1889. Poincaré was then 35. Hollywood was not even a dot on the map, and cinema at most a gleam in Edison's eye, but mathematics had that year an "Oscar," and he was all flesh and blood. His name was Oscar II, King of Sweden [O], the enlightened monarch who guided his realm through the difficult years when Norway clamored for independence, and who by his tact, wisdom and patience turned a bitter secession feud into a bloodless separation of the two countries. Since his early youth Oscar was enamored of mathematics, and on the occasion of his 60th birthday he announced an international contest [T] which carried a prize of 2,500 crowns and other awards. The winner of the prize was Henri Poincaré.
The subject of the contest was a problem which had agitated the mathematical world ever since Newton [N] had brought a host of inarticulate facts under a single principle, universal gravitation, and, by applying to these facts geometry and the calculus, turned Celestial Mechanics [M] into a branch of mathematical analysis. This was the beginning of a discipline which has since received the name of the problem of n bodies. It would have been more modest to call it problem of n points, because, by disregarding "internal" movements and deformations, the problem was restricted to the study of massive points subject to mutual attraction.
Newton solved the problem exhaustively for the case, n = 2. Two material points of arbitrary mass are placed into arbitrary positions, and are simultaneously hurled into space with velocities, arbitrary both as to direction and intensity. Assume the particles to be completely isolated from any influence other than their mutual attraction; assume this attraction proportional to the masses of the particles and inversely proportional to the square of the distance which separates them at the instant: what will be the state of the system at any subsequent time? [Pg 6]And when we say state we mean not only the relative position of the particles, but also their speeds and the directions which they follow at the instant.
The fact that Newton's solution of the 2-body problem [T] was in excellent agreement with the laws of planetary motion, which Kepler [K] had derived from observation and without the benefit of dynamical hypotheses, was a triumphal advance in the history of science. At the same time, this triumph eclipsed another issue raised by Newton, less spectacular, perhaps, but no less important.
Is the interplay of forces activating a system such as to vouchsafe perpetuity to the motions of the individual bodies? Could the mutual attractions between the bodies lead to aperiodic motions, or tend to rend the system asunder, or cause collisions, escapes, or both? The answer is that any one of these behaviors is possible, the history of a system depending on the intensity of the gravitational field, the masses of the participating bodies, their initial positions and initial velocities. These magnitudes are called parameters. Certain select values of these parameters induce regularity, periodicity, steady state, in sum, stability [S]. On the other hand, if these values be picked at random, it is far more likely that the motions would be irregular, even erratic, and may in the course of time lead to such cataclysms as collision or escape.
The problem of dynamical stability is twofold: first, knowing the parameters of a system, to determine whether the system is stable; and second, what conditions must be imposed on these parameters to assure the stability of the system. In the case of two bodies, these criteria of stability are implicit in Kepler's laws. It is quite different when the number of bodies exceeds two. Indeed, even in the case of three particles, the stability problem leads to difficulties which have taxed the ingenuity of many great mathematicians of the eighteenth and nineteenth centuries, and have not been completely resolved to this day.
I return to Poincaré. His prize memoir dealt with the 3-body problem [T]; but his approach to the problem and the [Pg 7]methods by which he attacked it were so broad in scope, that it can be said without exaggeration that he opened a new era in the history of celestial mechanics [M]. In a subsequent memoir he proved that among the infinite number of typical 3-particle configurations only 10 were stable. Later, after years of profound studies in the equilibrium of fluids and the theory of tides [T], he returned to the 3-body problem. However, this time he dropped the restriction that the bodies be rigid and immobile with respect to their own centers of gravity. By identifying the bodies with massive points, this restriction simplifies the problem materially; but this simplicity is achieved at the expense of actuality as is apparent in the important case Sun-Earth-Moon, to which, incidentally, the 3-bodies problem [T] owes its origin.
Poincaré's contributions to the n-body problem and kindred issues were incorporated in his treatise Lectures on the New Methods of Celestial Mechanics, the third and last volume of which appeared in 1893. The aim of this work was, to use Poincaré's own words, "to ascertain whether Newton's law of gravitation sufficed to explain all celestial phenomena." The advent of the Relativity [R] Doctrine has temporarily eclipsed this monumental work; which is not surprising since the new doctrine owed its very success to a spectacular critique of Newtonian mechanics. Today, the enthusiasm has dwindled to a point when it is more or less safe to assert publicly that, while classical mechanics is admittedly but an approximation to the "true" state of cosmic affairs, it is still quite adequate to deal with motions where the speeds are small as compared with that of light. This welcome sobriety may result in a renewed interest in Poincaré's work, and if and when this occurs, it will be realized that most of the issues which he raised sixty odd years ago remain unanswered today.
I have been delving of late in the works of Poincaré in the hope of finding in the style of his potent prose some clew to his elusive personality. This reading has led to an appraisal which I shall present here for what it is worth.
His prose is crisp, concise; it abounds in witty sentences, [Pg 8]clever metaphors and bold analogies; it unquestionably conveys to the reader what the author had in mind. With all that, it is not the polished elegant prose so characteristic of the French savant. Poincaré's writings hit the mark not through eloquent rhetoric or even cogent argument, but through shocks: bursts of unorthodox opinion, sweeping overemphasis, shafts of humor aimed less at some tangible adversary, than at genus homo at large.
His essays on the foundations of science are cases in point. They strike one as extemporaneous speeches rather than edited articles. As a matter of record, those who knew him best insisted that he rarely, if ever, would revise a manuscript, even if he was fully aware of its stylistic shortcomings. Poincaré himself expressed it as follows: "I never yet finished a work without feeling dissatisfied with the manner in which I had edited the work, or in the plan I had adopted."
What makes this casualness even more baffling is that Poincaré was an artist par excellence. Estheticism with him was not a mere creed: it was a way of life. "A savant worthy of the name," he wrote, "and especially a mathematician, has the same feeling towards his work as an artist: his joy is as great and of the same nature. I am addressing a public enamored of Science, or else I should have hesitated to say this for fear of arousing the incredulity of the profane. But here I can speak what I think: we work not only to obtain the positive results which, according to the profane, constitute our one and only affection, as to experience this esthetic emotion and to convey it to others who are capable of experiencing it."
That his crowded life left little leisure for the time-consuming task of editing a work—cannot be denied. But then why did he crowd his days as he did? His feverish activity, which I described earlier in this chapter, were not imposed by the exigencies of his position, nor was he one to be influenced by what the French so aptly call noblesse oblige. He certainly was not attracted by the lure of the limelight, or driven by the spirit of competition, for, indeed—to use a French phrase again—he was hors de concours. What was, then, the spirit and the urge which spurred his creative work? I believe that the answer [Pg 9]lies in a mental trait of Poincaré which, so far as I know, has not been brought out by his biographers.
To lose interest in one's work once the creative urge has spent itself—is a trait common to most creative minds. However, this loss of interest is usually accompanied by a sort of mental hysteresis, the subject haunting the mind long after the task has been consummated; this, and the natural exhaustion which follows in the wake of a continued mental effort, cause these long periods of hibernation which are so familiar and so frustrating to all who live by creative work. Poincaré's mind was not subject to hysteresis or hibernation. He had the unique faculty of dismissing an idea from his mind, the instant the stimulus was gone, and to supplant it immediately with another creative idea. This rare faculty may explain his apparent impatience with detail, the alacrity with which he could pass from one creative task to another. Above all, it may shed light on the extraordinary versatility of the man.
The brilliant Painlevé [P] depicted this versatility in an eloquent eulogy of which the following is an excerpt:
"Poincaré was indeed the living brain of rational Science. Mathematics, Astronomy, Physics, Cosmogony, Geodesy: he encompassed, he penetrated, he fathomed them all. Incomparable inventor, he was not content with following his own aspirations, by opening unexpected avenues and discovering unknown lands in the abstract world of mathematics. Wireless telegraphy, radiological phenomena, the birth of the Earth—whatever field man's reason had managed to invade, and however subtle, or however rough was the road, Poincaré, too, would invade it to help the searcher in his pursuit of the precious vein.
"Thus, with the disappearance of the great French mathematician has disappeared the one man whose thought could carry all other thoughts, the one mind who, through a sort of rediscovery, could penetrate to its very depth all the knowledge which the mind of man can comprehend. And that is why the demise of this man at the peak of his intellectual strength is such a disaster. Discoveries will lag, groping efforts will be drawn out; for, the potent luminous brain will not be there to [Pg 10]coordinate disjointed research, or to cast the daring plummet of a new theory into a world of obscure facts suddenly revealed by experience."
So much for the scientific work of Henri Poincaré. It is inseparable from his scientific philosophy, which is the thesis of the present volume. His contributions to science call for more space than what I have allotted here. Unfortunately, a more thorough analysis would exceed the scope of my undertaking, even if I had the space, which is not the case.
Of the scientific philosophy of Poincaré his eulogists give but passing notice. Philosophers, however, have not been so circumspect. Nominalism, conventionalism, idealism, realism, even solipsism and nihilism—were among the epithets hurled at him while he was alive; today, four decades after his death, the fury has subsided, and he is forgiven. But not forgotten: like the prophet of yore, he is invoked by many and followed by none. For, whenever a philosopher quotes Poincaré, the latter is not invoked to support the expert's own brand of reality, but to condemn a competitive brand. The scattered fragments of the tablets he smashed cannot be readily woven into a funereal wreath, but they make excellent missiles for metaphysicians at play.
As to Poincaré's scientific confrères, they regarded his philosophical outpourings as so much harmless eccentricity, much in the same vein as the family of a great artist accepts the capricious outbursts of their kin. A notable exception was his elder contemporary, Joseph Bertrand [B], who waxed quite indignant at an iconoclastic pronouncement of Poincaré which appeared in his treatise Electricity and Optics. Here is the passage:
"If a phenomenon is susceptible of one mechanical explanation, it is susceptible of an infinitude of others which would account equally well for all the features revealed by experience. . . . How are we to choose among all these possible explanations, when the aid of experience is denied us? The day will come, perhaps, when physicists will lose interest in these questions, [Pg 11]which are admittedly inaccessible to positive methods, and abandon them to metaphysicians. This day has not yet come: man does not resign himself so readily to ignore forever the essence of things. . . . Thus, the choice is guided by considerations in which the idiosyncrasies of the individual are paramount. Still, some solutions would be rejected by everybody as too bizarre, while other solutions would appeal to everybody because of their simplicity."
How would a modern physicist react to this pronouncement which, sixty odd years ago, caused so much commotion in the camp of the orthodox? Why, he would take it in the stride: the principle of indeterminacy [I]—of which, incidentally, the Poincaré statement was, in a sense, a forerunner—and other esoteric doctrines have inoculated these scientists against such shocks. Some physicists might even go so far as to regard the pronouncement as commonplace. "Truth," said Schopenhauer, "is a short holiday between two long and dreary seasons, during the first of which it was condemned as heresy, and during the second branded a platitude."
Strangely enough, the same physicists might be shocked by this other statement of Poincaré, which would be viewed as quite innocuous by a modern mathematician:
"Can one maintain that certain phenomena possible in Euclidean space [S] would be impossible in a non-Euclidean; so that experience, by confirming these phenomena, would refute directly the non-Euclidean hypothesis? To me such a question has no sense. As I see it, the question would be equivalent to that other, the absurdity of which is apparent: are there lengths which can be expressed in meters and centimeters, but could not be measured in fathoms, feet and inches; so that, by confirming the existence of these lengths, one could refute directly the hypothesis [H] that a fathom can be divided into six feet? . . . Thus, it is impossible to conceive a concrete experiment which could be interpreted in the Euclidean system, but could not be interpreted in the Lobachevskian [L]; from which we can conclude that no experiment will ever contradict the Euclidean postulate, [Pg 12]and, by the same token, no experiment will ever contradict the postulate of Lobachevsky. . . ."
One of his eulogists said that he had a posterity long before he died. I say that he had no posterity even after he died. He bequeathed to mathematics a land of prodigious promise, but the trails he had blazed were too difficult for lesser men to follow, and most of the problems he had projected will have to wait for another Poincaré to be solved.
Nor did he leave a philosophical posterity behind him. There are conventionalists, there are operationalists, there are non-positivists, there are even solipsists, but there are no Poincaréists. And for a good reason: one can talk solipsism [S], one can talk nihilism, one cannot live by such creeds. So fierce was the flame of Poincaré's creative joy that he could dispense with the tapers of realism. We, mortals, are not so lucky.
"No," he wrote, "scientific laws are not artificial creations; nor have we any reason to view them as contingencies, even though it is impossible to prove that they are not. Then, what about that harmony which human intelligence believes to have discovered in Nature: does it exist outside of that intelligence? Definitely not; a reality independent of the mind which conceives it, sees it or feels it is an impossibility. A universe as external as that would never be accessible to us, even if it did exist. For, what we call objective reality [R] is, in the last analysis, what is common to some thinking beings, and could be common to all: and this common part is the harmony expressed by mathematical laws. This harmony is the only objective reality, the only truth which we can attain; and if we remember that this universal harmony is also the source of all beauty, then we shall understand the high value one should place on the slow and painful progress which enables us, little by little, to learn this harmony better."
He was an iconoclast. But even in this category he defies classification. For, he fits no pattern, and is beyond all norm. He sought no followers, he shunned confederates, he hewed no tablets to replace those which he had shattered.
[Pg 13]He stripped the dingy icons off the walls of his cell, not to let in the light of the world without, but to uncover the mirrors which reflected the harmony within. He believed in that inner harmony, because he lived by it. He did not urge this harmony on others: "no secret can be told to any who divined it not before."
"The greatest contingency," he wrote, "is the birth of a great man." He was speaking of the laws of chance [C], and he had Napoleon [N] in mind. But his own birth was as great a contingency, and even greater was the forty years of uninterrupted peace which had fallen to his lot. Without that serenity there could have been no Poincaré. Today, no man could withdraw into an ivory tower and feast on the glory within, uninterrupted by the tumult without.
You heard the laments of his friends that he had died too soon. Now behold what he has been spared by dying on time. The din of the timbals was still in the air, when the grand debacle broke loose. For years war raged, killing, and maiming, and scorching the Earth. Then the aftermath: famine and pestilence, depression, defeat and decay. Again blind knaves driving blinder fools to gird their loins for a second Armageddon; all in the name of progress, peace and dignity of man.
I, for one, have lived long enough to know what he missed.
The industrial [I] conquests which enriched so many practical men would have never seen the light of day if these practical men had not been preceded by impractical fools who died poor . . . In the words of Mach [M], it was these fools who spared their successors the pain of thinking.
Henri Poincaré, On the Choice of Facts
THE evolution of scientific thought is inseparable from the history of man's efforts to resolve the perplexities of his own existence. Efforts to reconcile his ephemeral, fortuitous life with the will to permanence and certainty which obsesses his mind; his aspirations to grandeur and mastery with the insignificant part which he plays in the scheme of things; his apparent freedom to plan and strive with the inexorable operation of the causal chain of which he deems himself a link; to reconcile, above all, his inalienable belief that he is a part of the world with the awareness that he is a thing apart from it, an awareness for which consciousness is another name.
These conflicts have counterparts in scientific speculation. For, science itself may be viewed as man's supreme effort to find himself in that perplexing pattern which he calls Nature. Have three centuries of uninterrupted scientific and technical progress brought man nearer to the goal? Has he succeeded in achieving some measure of harmony with Nature? Or has he merely managed to transfer to Nature the irreconcilable duality within himself?
The future historian may call our period the great crisis. The ethical, esthetic, and intellectual standards which preceding generations viewed as firm realities are crumbling before our eyes. The political, economic, and social institutions which [Pg 15]have called these standards forth, and under which our ancestors lived in relative security, are giving way like levees under a mighty flood. At the same time a crisis is sweeping through the elaborate edifices erected by nineteenth century science; already one of these edifices has been shaken to its very foundations, and the process has just begun.
What are the sources of these upheavals, and what are their implications? To appraise the events that led up to these crises in their proper historical perspective, we must undertake a brief historical expedition into the golden age when hope was young.
Within a year of Newton's death, in 1728 to be exact, there appeared in London Ephraim Chambers' Cyclopaedia, an Universal Dictionary of the Arts and Sciences. It was not the first work of its kind, nor even the first in the English language; and while carefully enough compiled and well received by the public, its historical significance does not lie in the quality of the information which it disseminated or in the number of readers it reached. Its significance lies in the circumstance that, quite inadvertently, it gave the impetus to a movement which was destined to influence the outlooks of many generations to come, and which, in a sense, may be viewed as the intellectual precursor of the French Revolution.
It began with a few enterprising men [E] who decided to publish a French translation of Chambers' Cyclopaedia. When the project failed (largely because the French printer Lebreton tried to cheat his English partner), some of the younger editors conceived the idea of launching an independent work. The latter was eventually published under the title Encyclopédie, with Diderot as editor-in-chief, the first volume appearing in 1751 and the last in 1765.
The enterprise went through many vicissitudes. Individual volumes were confiscated, authors of articles persecuted, and even the crafty Lebreton, who to appease the censors would systematically mutilate the manuscripts by deleting from them everything that smacked of criticism of Church or State, even he did not escape a taste of the Bastille. When the work was [Pg 16]finally completed, its four thousand odd subscribers were ordered by royal edict to surrender their copies to the police, and the collection would have probably met its end in an auto da fe, had it not been for the timely intervention of Madame de Pompadour. According to Voltaire [V], the royal mistress had complained to Louis that the confiscation of the Encyclopédie prevented her from finding out how her rouge and silk stockings were made, and thus persuaded the king to return the seized copies to their owners.
Perusing the bulky volumes today, one marvels at the enormous success which the work unquestionably enjoyed. For the volumes are full of important gaps, the material is poorly documented; and as for the articles, some are undoubtedly brilliant, but many more are loosely conceived and badly executed. These defects were fully admitted by most of the editors and contributors. Thus d'Alembert [D], who wrote the introduction to the Encyclopédie, resigned his editorship with the scathing remark that the work was like a harlequin's coat: some good stuff, but mostly rags.
The names of some of the men associated with the Encyclopédie had much to do with its success: d'Alembert, Condorcet, Euler, Bernouilli wrote on mathematics and physics; Condillac, d'Holbach, Turgot on sociological topics; Montesquieu and Voltaire on philosophy and history; Diderot on the mechanical arts; Rousseau on music. Also, the traditional stupidity of censors contributed a great deal to the glamor of the enterprise. But while all this may account for the temporary success of the work, it certainly cannot explain the influence it exerted over subsequent generations.
The Encyclopedists left an indelible imprint on the minds of the intellectuals of their own generation and of the generations that followed, because they were exponents of the latent aspirations of these generations. They took an inventory of the thought and information accumulated since the Revival of Learning, and found it most gratifying. Not only had this progress led to a better understanding of man and the universe, but ample signs were at hand that soon this accumulated knowledge [Pg 17]would transform the life of man. This transformation, of course, could be only to the better!
This buoyant reliance on scientific progress was justified on historical grounds. Barely a hundred and fifty years had passed since Galileo's [G] experiment at Pisa had ushered in the new order of things; a mere instant as compared with the previous life of the race. Yet, this brief span had witnessed a complete shift in the outlook of the intellectual leaders of humanity: from blind adherence to authority and dogma towards a healthy habit of facing facts and an enlightened faith in the efficacy of reason. Few doubted that this buoyancy and self-reliance of the leaders would eventually reach the masses, thus causing a profound metamorphosis in the attitude of the common man towards his own life and the destinies of his race.
For, those were the days of the beginnings of technological progress. Research, systematic and painstaking, had begun to yield results. Materials which had lain inert in the bowels of the earth for millions of years were now uncovered, and were to be utilized for the benefit of man. The destructive elements of man's environment, the gods of yore, which had to be placated by prayer and sacrifice, were now to be harnessed to relieve human toil. Led by thinkers, and under the banners of liberty, happiness, and truth, humanity was to emerge into a Golden Age, free from oppression and strife.
Alas! The French Revolution [F] which followed close on the heels of the Encyclopedists resembled more a convention of inquisitors and hangmen than it did an assembly of enlightened emancipators. Those dreamers who had had the good luck to die before the great event preserved their illusions to the end. Those not so fortunate had their dreams cut short by the guillotine, the first labor-saving device introduced by the new order. After twenty years of adventure, the humanitarian aspirations bequeathed by the Encyclopedists, tattered and trampled first by a bloody republic, then by a still bloodier empire, were finally declared dead by the Holy Alliance.
Soon afterwards, another revolution [I], much more prosaic, but far more lasting in its effects, swept the Western world, [Pg 18]ruthlessly destroying standards which had grown so old as to appear eternal. But the Industrial Revolution, too, failed to introduce a reign of freedom and happiness: it converted the medieval serf into an industrial slave; replaced the feudal baron by the industrial mogul, created in its wake an ever-growing, ever-shifting class of declassés, who had neither pride of ancestry nor love of tradition, but who craved a place in the sun just the same. The age of machine and competition, of capital, class-struggle, and demagogy was upon man.
One part of the dreams of the eighteenth century intellectuals was realized: the resources of nature did yield a magnificent harvest. But the thinkers who helped to tap these re sources were not invited to the feast. Or were they invited, but failed to attend, detained in their studies and laboratories, lost in their dreams and calculations, seeking new fields, co-ordinating old and new, spinning abstract theories to explain the strange kinship between phenomena so different in content? Be this as it may, the thinkers were unequal to the task of developing these vast resources, most of which they had themselves uncovered. The shrewd declassés, who had nothing to lose—not even traditions—and the world to gain, pioneered this development and took possession of the earth.
In the course of this technical transformation, the attitude of the average man towards human destiny had undergone a radical change. To the man who lived before the Industrial Revolution life was essentially static. He would die in the state which had been his at birth, and the same was true of his neighbors, friends, and masters. Nothing, indeed, occurred in his own lifetime which did not happen to his father and grandfather, unless it had been a calamity, such as drought, flood, plague, war. No change was desirable. For, was there ever a beneficial change? Life was hard, very hard! But a change would make it still harder. Let well enough alone!
Man was like a plant which grew from seed, reached its height, and died with the first frost. What could occur to upset this routine? A worm might destroy it at the root, a blight might affect it at the stem, a beast might crush it. Any change [Pg 19]from the regular routine was a calamity. Could the plant prevent such a calamity? Neither could man. For [E] all was in the hands of Fate. And Fate was like a cruel tyrant who persecutes and flays and robs his subjects, but who expects these subjects to tell him daily that he is just, generous, merciful. Before such Fate man was a beggar and a thief. He stole from Fate a mite of bliss and lived in abject terror lest his crime be found out; he eased his guilty conscience by confessing and repenting.
The striking effect of the Industrial Revolution on the common man was the proof that change was possible, and that it was not necessarily a calamity. It was not a theological proof, the kind his minister used in demonstrating that the Deity was good and benevolent, despite that life had failed to confirm it. It was a pragmatic proof: he saw the consequences of these assertions before his own eyes. He saw his own ambitious neighbor escape from poverty and humility into the master class. Born humble, the parvenu died amidst luxury and pomp, leaving his children in affluence and power.
He saw his countryside transformed, and not by a hurricane or flood, but by railways and hydraulic plants, mills and factories and mines; later by telegraph, telephones, and motor cars. Irrigation and artificial fertilizers made droughts less calamitous; sanitation and antiseptics made epidemics less frequent. True, many of the old evils persisted, but a way will be found to eliminate these too. Step by step, he began to lose his former supine submissiveness. Timidly, at first, but with increasing courage he began to think of himself as of a free agent. As an individual he was still subject to the vagaries of existence, but as a member of the human race he had come to think in terms of progress.
Eventually he swung to the other, the buoyant extreme: man was the captain of his ship, he was the master of his fate. True, fate was not benevolent to man, but neither was it hostile: it was merely indifferent. Ignorance was the one real obstacle, and this could not be overcome in a day. As man would penetrate deeper and deeper into the secrets of nature, he would learn to defend himself against the calamities before which his [Pg 20]predecessors had stood helpless. Nay, he would tame these wild destructive agents and turn them into beasts of burden as it were. One by one, he would eliminate from his life the fortuitous elements which cause so much misery and insecurity. Do you doubt it? Look out of the window and observe what a single century of systematic unhampered application of science has achieved! The pragmatic force of this argument would silence the most hardened skeptic.
We owe to the experimental method [E] this remarkable metamorphosis of the human spirit which in the brief span of two centuries had turned a herd of abject slaves into crusaders who aspired to partnership with destiny. The machine age had opened to the masses vistas which were beyond the wildest dreams of the Encyclopedists: the conquest of nature had just begun, and who would be so bold as to prophesy where it would end.
To be sure, these dreams were not without their nightmares. Time and again man would be reminded, through floods, droughts, and pestilences, through wars, panics, and depressions, that he was not yet the master of fate. But the spirit, once liberated, would not be downed. The inventive genius of the race will find ways to conquer these recurring calamities of nature, while education and organization will eventually wrest from the privileged few their control of production and distribution. With the power vested in an enlightened State, war and depression would become mere memories, and poverty and scarcity just relics of a bygone age. For, there is no ground for scarcity in a world of abundance, and the earth is abundant. Its resources have barely been tapped: remove the shackles which an obsolete order has fastened on progress, and biology, chemistry and mechanics will do the rest. Thus spake the buoyant of spirit!
History of Science reveals to us two kinds of phenomena, opposite as it were: at times, simplicity [S] is hidden behind apparent complexities; at other times, on the contrary, we find that behind apparent simplicity hide extremely complicated realities.
Henri Poincaré, Hypotheses [H] in Physics
THIS conquering spirit found its counterpart in scientific speculation. For, here too a conquest was taking shape, more abstract in character and hence less conspicuous, but in the end just as bold and sweeping. Imperceptibly at first, but with growing tenacity, mechanics [M] was emerging as arbiter between scientific theory and mathematics.
The story harks back to the Pythagoreans [P] and their dictum "Number rules the Universe." Memorable battles were fought by the Sophists against this reduction to number. Parmenides and Zeno [Z] directed against the philosopher-mathematicians of their day a scathing critique the echo of which has not subsided to this day. The celebrated Zenonian paradoxes of motion should indeed be interpreted as a protest against the mathematical method which tends to reduce motion to a mere correspondence between space and time. Zeno maintained that there was in motion a certain quality which no amount of mathematical juggling will absolve.
Whatever commotion the Sophists might have caused among their own philosophic contemporaries, on the history of mechanics they exercised little influence. It is true that, with the exception of Archimedes, the geometers of the subsequent period displayed little interest in matters mechanical. This, however, was due not to the incongruities revealed by Zeno, but to the esthetic compunctions and aristocratic tendencies of [Pg 22]the Greek mathematicians. It was not that the geometers of antiquity had failed to implement the concepts of mechanics, but that the mechanics of their period had no concepts to implement.
Founding the science of mechanics was Galileo's [G] achievement. It was he who first introduced the concept of velocity in non-uniform motion, that of acceleration and force, the principles of inertia and of relative motion, and other ideas which play fundamental roles in modern dynamics.
French geometers took up these problems where Galileo had left them and carried them far afield. However, for its real triumphs the science of mechanics had to wait until after Newton [N] and Leibnitz had systematized the methods of the infinitesimal calculus. For, mechanics was the vast proving ground on which these new mathematical weapons were tested and perfected.
Newton's Principia furnished the chief impetus to this development. Here the fertile ideas of Galileo, the astronomical discoveries of Kepler, the analytic geometry of Descartes, and the newly forged tools of mathematical analysis were for the first time welded into a sweeping synthesis. But even more important was the fact that Newton applied this mathematical apparatus to universal gravitation: for, the brilliant success of that theory lent to the method great pragmatic force.
In this manner was launched the movement which we may call mathematization of the physical sciences. Henceforth, the task of reducing the physical universe to number was to be materially simplified, inasmuch as it meant recasting physical entities into terms of the basic concepts of mechanics: space, time, matter, force, and energy.
The subsequent history of theoretical physics may be interpreted as gradual subordination of its various branches to this one central discipline, mechanics. At first this movement progressed rather slowly; but in the middle of the nineteenth century the mechanistic tendency received a powerful stimulus from the discovery of the principle of mechanical equivalence [E].
[Pg 23]According to this latter, energy [E], whatever might be its form or source, i.e., whether it be derived from heat or chemical change, sound or light, electricity or magnetism, was always equivalent to a proportional amount of mechanical work. The principle assigned to every form of energy a specific numerical constant, called the mechanical equivalent of that form of energy: this served to convert any quantity of that energy into a corresponding amount of mechanical work, very much in the same way as one converts yards into meters. From this to a potential mechanization of all physical units was not very far, and, indeed, in the course of the following half a century all physical measurements were, one by one, reduced to the fundamental units of mechanics.
Thus all physical phenomena became linked in a vast process of transformation, any individual phenomenon being viewed as but a particular phase of the process, expressible in the same terms, and measured by the same units as any other. Upon energy was bestowed the function of unifying agent. To be sure, in the early stages of this evolution the equivalence of the various energies might have been regarded as more or less formal. But it could not be expected that such modesty would last, and it did not: within a decade of its discovery the principle of equivalence became that of conservation of energy.
When one endeavors to analyze the methodology of classical physics, he is at first struck with its complexity. After a while, however, one begins to discern in this intricate pattern a few basic, continually recurring ideas. Among these I shall particularly mention conservation [C] and what may be called economy [E], inasmuch as it commonly involves the notion of minimum. A naive intellect who would accept this terminology at face value might conceive Dame Nature as a thrifty housewife who had vowed to practice rigid economy in the dispensation of some resources, while jealously watching that other resources be left intact.
From the mathematical point of view, either principle leaves little to be desired. A principle of conservation identifies a physical phenomenon with a mathematical form which must [Pg 24]retain its magnitude for all values of the variables involved; a principle of economy [E] identifies a physical law with the conditions that a certain mathematical function attain a maximum or a minimum, as the case may be. Thus both serve to convert physical problems into forms susceptible of mathematical treatment. Or, if we are to adopt the skeptical attitude of Nietzsche, both principles belong to the grandiose gear by means of which science is endeavoring to "counterfeit Nature through Number."
As to which of the sundry attributes that man has read into her, Nature is bound to conserve or economize depends largely on the period studied. In the earlier days, the object of conservation was matter; later it became energy, then mass-energy; today it is momentum, I believe. The principle of economy underwent similar fluctuations: Fermat [F], who was the first to guide physics into this path of inquiry, held that among all the possible ways in which Nature could discharge a function, she invariably chose the one which required the least interval of time; to Maupertuis [M] it was not time, but a certain intangible entity, which he called action, that was the object of Nature's thrift; today, the principle of least action still stands, except that the Maupertuis concept has been abandoned in favor of a broader idea introduced by Hamilton [H].
The principle of conservation of energy, as formulated by Simon Newcomb [N], states that "No form of energy can ever be produced except by expenditure of some other form, nor annihilated except by being reproduced in another form. Consequently, the sum total of energy in the universe, like the sum total of matter, will always remain the same."
It appeared as though the universe was filled with an intangible cosmic substance which for some mysterious reason Nature had pledged to conserve. This substance was the counterpart of matter, and yet in many respects it resembled matter. This resemblance was later to serve as the point of departure for the erection of a unitary theory in which energy and matter become virtually interchangeable.
Still, even this universal principle was unable to explain completely the strange kinship between phenomena so different [Pg 25]in content. The theoretical physicist longed for a mechanistic interpretation of this kinship; he sought a mechanism which would incorporate all these transformations. Seek, and ye shall find! It was not long before these efforts had crystallized in the various theories of matter: the molecular, the atomic, and finally the electronic. Of this, however, later.
By the end of the nineteenth century, this process of mechanization of physics had been consummated; the recognition of mechanics as the universal unifying agency seemed justified in all fields of physical activity. In the microcosmos, the universe of small-scale phenomena, the mechanistic hypothesis had led to theories which were successful not only in interpreting known facts, but, by their brilliant forecasts, had guided experiments toward new discoveries. In the macrocosmos, the field of large-scale phenomena, astronomy, guided by the laws of celestial mechanics, had succeeded in interpreting with marvelous precision the known movements of the heavenly bodies, and in foreshadowing the existence of new bodies on the basis of the perturbations observed in the courses of those previously charted. Finally, the colossal engineering accomplishments of the machine age testified to the power of mechanics in matters terrestrial.
To be sure, there remained phenomena which had thus far resisted all the interpretations on the principles of classical physics. Yet it was confidently believed that these difficulties too would be eventually overcome: a more intimate knowledge of the underlying mechanism would succeed in bridging these gaps, as other gaps had been hitherto bridged. It was generally felt at the turn of the century, that fundamental discoveries pertaining to both principles and methods were largely matters of the past; that from now on there would arise only questions of details, of refining the existing methods; or, as one physicist had remarked, a question of adding a few more decimal places to the values of the physical constants.
Science, it was thought, had reached a position of stable equilibrium. Revolutionary disturbances were unlikely, and the days when the prophetic insight of a genius could rock the [Pg 26]foundations of the scientific edifice were definitely over. Guided by the immutable principles established by the pioneers, science might now settle down to the painstaking details so dear to the average mind. This task, moreover, could be entrusted to the drawers of water and hewers of wood.
Yes, serenely calm was the outlook of classical physics at the opening of the new century. Behind it lay a record of achievement without parallel in the annals of progress; ahead lay a rich field of endeavor which had already been partly explored. The pioneers had surveyed the vast territory, and no surprises were expected. There remained the task of staking it out and distributing it among the great army of scientific workers trained in principles and methods rigorously formulated by the masters, and thoroughly tested in the exacting school of experience.
These principles had mapped a closed universe in which causality reigned supreme. This universe was actuated and regulated by immutable laws of a rational character. Mathematical simplicity was the key to this rational code; experience was the ultimate judge of all interpretations by this code; by means of these criteria errors of judgment could be eliminated and illusions due to human foibles discounted or dispelled.
The closed universe of classical science was like a huge mechanism [D]. The mechanism operated in an immobile and immutable spatial framework of cosmic proportions, subject to the rigid laws of classical geometry; it was pulsating in synchrony with a cosmic clock. Within this framework and attuned to the cosmic rhythm, the mechanism was in incessant flux: in the vast reservoir of matter and energy, the ingredients were constantly seething, changing, moving, transforming. Yet, not all was in flux: there was the fixed, the permanent, the absolute [A]; the vantages to which the seething universe could be referred, the entities in terms of which it could be expressed. For, the pattern of cosmic evolution was invariant; and so were the universal constants; matter and energy were indestructible; the spatial framework was firmly fixed, and the chronometer of duration ticked-with absolute uniformity.
[Pg 27]It was not a mere universe of discourse; nothing seemed more solidly anchored to firm reality. The physicist sat in his laboratory and watched physical reality pour in through the windows; it kept clicking his apparatus, kept indicating numbers on his graduated scales, kept actuating the styli of his registering instruments. Here, charted on the walls of his laboratory in formulae, diagrams, graphs, and tables, was reality itself. For, have not appearances and delusions been screened out by the very design of the instruments? Have not the systematic errors due to sense-illusions and personal equations been discounted by means of the mathematical theory of probability?
Nor was this science a mere intellectual game; it was a serious business, a campaign aiming at the conquest of Nature. On it rested the hope of humanity, the welfare of the multitudes, the elimination of fortuitous elements which have so often in the past bedeviled the life of man; a clearer understanding of the universe and of the part which man played in it. Science would not betray this trust!
The ship of man was sailing, sailing towards happier shores. Captain Science stood at the helm: competent and confident, he peered steadfastly at the immense expanse on which his vessel seemed but a forlorn chip. He believed in himself, for had he not nearly unraveled the intricate pattern of this vast and turbulent ocean? Confidently and competently he kept charting the course of his craft.
What the astronomer calls a straight line is, after all, just the trajectory of a ray of light. If then it was found that some parallaxes were negative, or that all parallaxes were above a definite limit, we would have to chose between two decisions: to renounce Euclidean Geometry [G], or admit that light does not travel along rigorous straight lines and modify the laws of optics accordingly. It is useless to add that people would regard the second decision more advantageous. Thus, Euclidean Geometry [G] has nothing to fear from new experiments.
Henri Poincaré, Experience and Geometry
THE Creator has with one majestic sweep arrested all motion. The Universe is at rest, frozen as it were, every particle in it occupying that position which it had at the instant all ceased.
The Creator takes the inventory of His Universe. With straight and rigid, yet infinitely long and infinitely thin rods, He erects an imponderable scaffold. This scaffold pervades the Universe: at every point meet three of these rods, one running up and down, one North and South, one East and West.
The Creator now chooses a center for His Universe. Some point, say in the Holy City of Rome to which He has shown such marked preferences in the past, He selects for His absolute post; this from now on and unto eternity shall serve as the universal center of reference. From this absolute center, and with an absolute unit of His choice, He measures the distances of every point along these absolute directions of His scaffolding. The numbers thus obtained He inscribes on an imponderable label attached to the point. Every point in the Universe has a label all its own; on this label are inscribed three numbers, which from now and unto eternity shall serve as the absolute [Pg 29]coordinates of the point. And at every point of His Universe the Creator places an imponderable clock, all clocks as yet pointing to zero time.
Having thus completed the inventory of His Universe, the Creator with another sweep sets it back into motion. The imponderable clocks begin to tick in perfect synchrony, all clocks pointing to the same time, absolute time. The earth resumes the spinning about its axis and its journey around the sun: the other planets, too, resume their revolutions, the sun its flight towards the constellation of Hercules, Hercules, in turn. . . . In short, the Universe returns to the peregrinations interrupted by the Divine survey, as though nothing has happened, ignoring what has happened; not aware of the universal inventory that has taken place. So the Creator has willed.
Rome is not the absolute post any more. It is engaged in describing a composite trajectory, and every instant removes it further and further from the universal center which has once graced it with coincidence. Yet for the Divine Observer at His absolute post there is no mystery about this complex motion. For, as the dome of St. Peter passes some point in absolute space, it registers the absolute coordinates of the point, and clicks off the absolute time of the passage. And the same holds for any particle of the vast Universe. It is, indeed, as though every particle in its complicated flight is following a thread all its own; on this thread are strung infinitely small beads, and as the particle passes such a bead it imprints on it the time of its passage. This thread, frozen as it were, on which are strung in infinitely dense formation timing numbers, tells the absolute history of the particle, and the totality of these beaded threads constitutes the absolute history of the universe.
What is wrong with this scene? Only this: it required a deity to stage it, whilst mere man must run the show! And it is not given to man to possess an absolute to which he can refer his fleeting impressions of a universe floating in space and time, the only universe he knows. Not that he did not strive to attain this absolute: the history of culture is replete with the quest, and more than once man thought that he had at last [Pg 30]attained the goal, only to discover that he had been pursuing a mirage.
A babe, immobile in its cradle, just awakening to the consciousness that it is not one with the world surrounding it, may regard itself as this absolute about which the world is moving. A plant-like being endowed with intelligence to draw conclusions from recurring events could think of the spot to which he is riveted as of the center of his universe; his right and left, his fore and aft and his up and down might appear to him as the directions singled out by nature as of absolute importance.
Should he commune with his plant-like neighbors, his conviction in the absolute character of the vertical would be confirmed; on the other hand, his egocentric ideas about his right and left and fore and aft would be shattered, for, he would learn to his dismay that each one of his neighbors as stubbornly maintained that his own physiological specifications had been so selected by nature. If now by some miracle this plant-like population were to be granted mobility, what a revolution this would cause in their outlook!
It is unlikely that our ancestors had ever cherished such egocentric illusions, at least not in matters of geometry. Yet the idea of the absolute nature of the vertical persisted as long as the flat earth was regarded as immobile in space. Came the time when this geocentric hypothesis had to be sacrificed on the altar of mathematical simplicity. The absolute center was then moved to the sun, and man thought that the long quest had at last come to an end. Yet scarcely two centuries passed, and the heliocentric hypothesis [H] too became incompatible, this time with the vaster cosmography of interstellar spaces: the center of the universe was again moved, this time to some vague point in the northern celestial hemisphere, toward which our solar system appeared to be moving with a velocity exceeding by far that of its fastest planet.
Thus the post from which we observe the universe, far from being immobile, is spinning about an axis which, in turn, revolves about a center, while the latter is itself in flight, perhaps, as a part of a still vaster system which, for all we know, may [Pg 31]be engaged in a still more complicated motion. Hence, even granted that absolute space "exists," we have no means at our disposal of discerning our position with regard to it: overnight the whole observable universe might have drifted into another portion of this absolute space, without our being made to the slightest degree aware of the transition. Clearly, no physical reality can correspond to such a conception of space; and, as we shall see, we are not better off in regard to the conception of absolute time.
Yet classical physics had posited these two concepts at the very basis of all physical theory. For more than two hundred years the concepts of absolute space and absolute time were invoked, overtly or tacitly, to interpret physical experience. And, barring a few apparently disconnected cases, facts and theory did dovetail with tolerable precision. Is it not paradoxical that what appears to us today as unwarranted assumptions of an unverifiable character have yielded such remarkable results for so long a period?
The first systematic treatise on classical dynamics was Newton's [N] "Mathematical Principles of Natural Philosophy," published in 1686. In the first Scholium of these Principia we find the following passage:
"I shall not define time, space, place or motion, for, these are well known to all. I must observe, however, that the vulgar conceive these entities only in their relation to sensible objects. This has given rise to many prejudices, to remove which it will be convenient to distinguish between the absolute and the relative, the true and the apparent, the mathematical and the common."
"Absolute, true, and mathematical time, of itself and from its own nature, flows equably without regard to anything external, and by another name is known as duration [D]; relative, apparent, and common time is some sensible and external, whether accurate or unequable, measure of duration through motion. . . ."
"Absolute space, by its own nature and without regard [Pg 32]to anything external, remains always similar to itself and immovable. Relative space is some movable dimension or measure of absolute space."
Clearly, Newton [N] did not intend these statements as definitions of time and space, for, he regarded these concepts as common notions understood by all men and, therefore, requiring no definitions. Should the statements, then, be interpreted as positing the existence of a reality behind mere appearances? Newton himself would have answered this question with a firm "HYPOTHESES NON FINGO." I quote from the last Scholium of Principia: "Hitherto I have been unable to deduce the cause of gravity from phenomena, and I frame no hypotheses; for, whatever is not deduced from phenomena is to be called an hypothesis [H]; and hypotheses, whether metaphysical or physical, whether of qualities occult or mechanical, have no place in experimental philosophy."
HYPOTHESES NON FINGO. This famous phrase, inscribed on one of Newton's portraits, rings strangely in modern ears. And even stranger sound his allusions to the "vulgar." The tables are turned. It is the professional physicist who seeks to reduce time and space to such "sensible" objects as clocks and gauges, while the "vulgar," the layman, is content to view these concepts as eternal realities which exist "without regard to anything external," and which, indeed, would continue to exist even if all human activities, nay, thought itself, would perish.
Newton's appeal to absolute space was not unlike a pious declaration which ushers in the labor of a day, but which has no other bearing on the forthcoming day's labor. For, having invoked absolute space, Newton summoned classical geometry as a method. More than two thousand years had elapsed since Euclid had gathered the geometrical knowledge of his time into a comprehensive treatise. In these two thousand years, the treatise became the source and inspiration of mathematical activity. Like his predecessors, Newton accepted it unqualifiedly not only as a foundation for geometry but as a model of perfection for other sciences to emulate.
Now Euclid too had postulated certain attributes of space, if not in explicit statements, at least in tacit assumptions. What is more, Euclid [E] used his assumptions; used them so well, indeed, that they finished by permeating the whole edifice of classical geometry. However, Euclid's space was not the absolute space of a Divine Observer: it was the relative space which man, "cooped under an inverted bowl," had evolved in his age-long efforts to reconcile the static perceptions of his senses with his own mobility and the ceaseless changes in his environment.
This space was homogeneous [H] and isotropic [I]; not that Euclid used such sophisticated terms, but that these were certainly implied in his definitions, axioms, and "common notions." Euclid's [G] space was homogeneous, because any point in it was geometrically indistinguishable from any other point; it was isotropic, because any direction in it was geometrically indistinguishable from any other direction.
Because there were neither preferred points, nor preferred directions, nor yet preferred localities, any rigid figure could be freely transported from one position to any other position in space without this displacement affecting even to the slightest degree the geometrical aspects of the figure; as, for example, the distances between its various points, or the angles between its constituent lines. On this invariance of geometrical properties under displacement were based the criteria of congruence [C] of figures; on these criteria, in turn, and on those of similitude, rested all of classical geometry.
Now, this postulate, that displacement does not affect the geometrical properties of a rigid body, may be designated as principle of relativity [R] of classical geometry. Indeed, it is equivalent to the statement that it is impossible by the methods of pure geometry to ascertain the position of a body in absolute space; and this is tantamount to declaring absolute space beyond the jurisdiction of geometry, pledging geometry to the study of relative properties only. To other considerations may be left the determination of the absolute position of a body: so far as geometry proper is concerned, absolute space is void of meaning; [Pg 34]for, in matters scientific an assumption without consequences is an assumption without significance.
Thus, when Newton accepted the classical geometry of Euclid as a cornerstone of his system, he, by the same token, pledged himself to use relative geometrical properties only, and to that extent at least his preamble on absolute space was but a pious invocation. But this was not all: this unqualified acceptance imposed on Newtonian cosmography still another restriction, even more exacting in character. Indeed, the metric aspects of classical geometry, the theory of magnitude and measure, proportional division, the inter-relation between distances, angles, arcs and areas, and the many other relations which Newton had used with such telling effect in erecting his system, depended for their validity not only on the existence of congruent figures, but on that of similar [S] figures as well.
"Similar rectilinear figures," says Euclid: "are those which have their several angles equal, each to each, and the sides about the equal angles proportional." The independence of the two conditions of similarity—the congruence [C] of angles, on the one hand, the proportionality of rectilinear elements, on the other—is an essential aspect of the theory. Both conditions are necessary; neither is sufficient in itself. Thus, two rectangles may be dissimilar, although the corresponding angles are certainly congruent in this case; again, the sides of any rhombus are certainly proportional to the sides of any square, and yet the two figures are generally dissimilar. Angular congruence does by no means entail proportionality of lines.
The case of two similar triangles is an important exception. Here the congruence of corresponding angles does entail the proportionality of corresponding sides and, consequently, the similarity of the two figures. This property of similar triangles enabled Euclid to eliminate allusion to proportion and reduce the criteria of similarity of two polygons to congruence tests.
The procedure is analogous to the one used in the case of congruence: by resolving the two figures into an equal number of component triangles and invoking the principle that the similarity of component parts entails the similarity of the resultant [Pg 35]configurations, one may reduce the problem to ascertaining whether certain auxiliary angles are congruent. That analogous procedures are followed in both problems is not surprising if we but reflect that from the mathematical point of view congruence is a particular case of similitude, the relative magnitude of two congruent figures being 1.
If overnight all the dimensions in the universe would increase thousand-fold, the world would remain similar to its former self, the term similitude [S] being used here in the sense of Book Three of the Elements. Only, what was once a meter long would now measure a kilometer, and what was once a millimeter would be now a meter. The bed in which I slept and my body would increase in the same proportion. How would I feel when I awoke in the morning in the wake of such an astounding transformation? Well, I would perceive nothing at all!
Henri Poincaré, The Relativity of Space
ONE of the most striking features of Euclid's geometry is that the existence of similar figures was made to depend on the existence of parallel lines, i.e. "straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction." As to the existence of parallel lines, it was sanctioned by an axiom which has since come to be known as the Euclidean postulate of parallels [P].
The postulate of parallels was the fifth in order of presentation. The preceding four were regarded by classical geometers as mere principles of construction, asserting the right to use the straightedge and the compass as geometrical instruments. The fifth postulate, however, did not possess in their eyes the same degree of evidence, and was treated for this reason as an unproved theorem. Thus in the course of the next two thousand years futile attempts were made to deduce the proposition from the other axioms.
Most of the would-be proofs began with replacing the fifth postulate by one or another of its numerous consequences, [Pg 37]such as: if in a quadrilateral three angles are right angles, then the fourth angle is also right; the sum of the angles of a triangle is equal to two right angles; it is possible to construct a triangle the area of which exceeds any magnitude assigned in advance; the square on the hypothenuse of a right triangle is equal to the sum of the squares erected on the sides; it is possible to construct a triangle similar to a given triangle and yet not congruent to it.
This last proposal is of particular interest. It was made by John Wallis [W], the teacher of Isaak Newton, in a lecture delivered at Oxford University in the year 1651. Whether or not Wallis believed that the existence of similar triangles was a consequence of the other postulates, common notions and definitions posited in the Elements—is not on record. He did, however, establish the complete equivalence of the two versions, by proving that if the assumption that similar triangles exist be adjoined to the other axioms, then the existence of parallel lines would follow as a logical necessity.
Two questions arise at this juncture. The first is: What relation can there be between similitude [S] and parallelism? What has the existence of lines which never meet to do with the existence of figures which differ in magnitude, but not in form? The second question is: What guarantee have we that similar figures exist at all? The formal apparatus known as the theory of similitude merely assures us that if such figures did exist, they would have such and such properties; it does not give us the assurance that similar figures actually exist.
Euclid [E] answered these questions in Book VI of the Elements. The book is headed by a proposition which links similitude and parallelism, and at the same time proves the existence of similar triangles by actually exhibiting a pair of such triangles. For, it should be remembered that from the existence of a single pair of similar triangles the existence of an infinite number of similar triangles may be inferred, inasmuch as by displacing one or both triangles, we obtain new pairs of triangles which remain similar. Again, by composition, we may infer from the existence of similar triangles the existence of similar [Pg 38]polygons, and from this, by limiting processes, derived the existence of curvilinear figures.
The proposition just mentioned may be formulated as follows: if a line be drawn which intersects two sides of a given triangle and is parallel to the third side, this line will separate from the given triangle another triangle similar to the original. Not only, therefore, does this theorem prove the existence of similar triangles, but it offers an actual method for constructing any number of triangles similar to a given triangle.
Now, existence [E] means one thing to the physicist, quite another to the mathematician. Whether a thing exists or does not exist is to the physicist a matter of experimental evidence; to the mathematician, on the other hand, existence is co-extensive with freedom from contradiction. The position of mathematics with regard to the question at issue is this: similar figures exist, if the postulate of parallels is valid; and the postulate of parallels is valid, if it does not contradict the other premises of classical geometry.
How about the physicist? Well, consider an hypothetical physicist who has pledged himself to use only such notions and concepts as can be translated into terms of experience; and when I say experience, I mean direct observation reinforced by instrumental procedure. This physicist undertakes to revise the Euclidean Elements with the view of adapting them to his experimental technic. He accepts the principle of congruence, for the latter implies only such ideas as displacement and rigidity [R], and these ideas are among the credos of his own catechism. On the other hand, he rejects the notion of indefinite extension, or anything that smacks of it, as something which is a priori impossible of execution: hence the phrases "if continued far enough" or "however far continued" are to him void of all physical significance.
Eventually he reaches the definition of parallel lines: two lines are parallel if they do not meet, no matter how far extended. This sounds to him as so much conjuring. To test whether two lines are parallel or not he would have to spend the rest of his natural life, and on his death-bed bequeath the task to generations [Pg 39]to come. The phraseology of the postulate of parallels appears to him just as objectionable.
"Either," he ponders, "one can purge the concept of parallelism from all such 'theology,' or else one must abandon it, 'bag and barrel.'" Frankly, the second alternative seems more practical. However, as he reads on, his objections become less vehement. Is it possible that Euclid had used his conjuror's art merely as a means to an end? For, out of the hazy mist where only a god could navigate emerge conceptions which mortal man can grasp and even test; not just abstractions invoking the infinitely remote which is a priori inaccessible to observation, but statements dealing with local properties of things which are amenable to verification.
"It matters not," he argues, "that Euclid had invoked such terms as indefinite extension. His appeals to the infinite were mere figures of speech. Indeed, the infinite has many local echoes, and similitude is one of these. The verdict as to whether similar triangles exist falls within my jurisdiction of a physicist. Innumerable observations and experiments have established beyond peradventure the existence of triangles which have equal angles but unequal sides; and incontestable measurements have proved that the corresponding sides of such triangles are invariably proportional. Mathematicians have assured me, on the one hand, that similitude and parallelism are logically equivalent assumptions, and, on the other hand, that parallelism does not contradict the axioms of congruence [C]. Thus, I can accept without qualms the whole apparatus of classical geometry, disregarding references to the infinite as useless, but also harmless, phraseology consecrated by tradition and habit."
The position of mathematics with regard to the basic premises of Euclidean geometry is summed up in the verdict: similitude is compatible with congruence. The verdict of physics is: observation and experiment confirm the existence of similar as well as of congruent figures. Both vindicate Euclid and the Greek geometers for whom he acted as spokesman, and Thales [T] of Miletus, the creator of deductive geometry, who founded the science on the criteria of congruence and similitude.
[Pg 40]It was not logic that had guided these men in their choice, but that undefinable complex of collective predilections which we call intuition, and which the Greeks strangely enough called aesthesis. And this is but another way of saying that the geometer had no choice in the matter, that the choice had been predetermined long before premises and postulates emerged to become parts of human discourse, predetermined by that hypothetical remote ancestor of ours who first conceived FORM [S] as distinct from POSITION and MAGNITUDE. [S]
Our intuition discerns these aspects in any situation which calls for geometrical judgment, but these aspects are not of equal portent: we regard form as intrinsic, innate; position and magnitude as adventive or casual. If you ask me to describe an object, and I should say that it is situated in such and such a place, or that it occupies such and such a volume, you would adjudge my answer as stupid, or trifling, or both; if, on the other hand, I said that the object had the shape of a sphere or of a cube, you would find my reply to the point. The first principle in classifying geometrical beings is form: position and magnitude are rather irrelevant, and in a sense trivial. This, indeed, is what we mean by similar: alike in all intrinsic traits, distinct in traits irrelevant.
The grounds for the priority which our intuition bestows on form are manifold, but they all derive from the belief, universally shared by all normal men, in the existence of rigid bodies. What is the source of this unanimity? What leads us to declare certain objects in our environment to be geometrically permanent, while recognizing at the same time that certain other objects lack this stability in form, or in magnitude, or in both? I know no answer to these queries except the time-worn maxim that man is the measure of all things, and that there is no other measure. When viewed as a geometrical being, man is but an articulated system of quasi-rigid limbs: his own body serves as the standard of rigidity [R] which he instinctively and incessantly applies to the world around him. A rigid object is one which is sensibly invariant in relation to his own body: that is why his judgment as to what is rigid or not appears to him so spontaneous and so infallible.
[Pg 41]We may rephrase this theory to spare the feelings of those who become irritated at allusions to the anthropomorphic origin of concepts. We may say, for instance, that space is homogeneous and isotropic; or that it is so constructed as to offer no resistance to the movement of rigid bodies; or that any two portions of space which at different times are occupied by the same rigid body are congruent to each other. Still, re-phrase it as we may, it is the belief in our own free mobility [M] that lends to any one of these statements its pragmatic force.
No man sound in mind and body has ever entertained doubts as to this neutrality of space towards motion. The mere fact that he can displace his body without experiencing pain is to him sufficient proof of that passivity. Conceive, on the other hand, of a species of intelligent beings so afflicted from birth that the slightest movement of any limb in their bodies would be accompanied by pains and contortions. Would these beings too be led to postulate the benevolent neutrality of their theatre of activities? No. They could not even conceive displacement, i.e., motion without deformation, and if they were inclined even as you and I, to bestow on their predilections the dignity of laws of nature, they would finish by finding in the structure of their space the source of their limitations.
And just as we postulate free mobility [F], meaning by it that we can displace a rigid body without changing it either in form or in magnitude, so do we postulate free expansion and contraction. We conceive physical space so constituted as to offer no obstacles in the way of growth [F] or dwindling. Just as space is indifferent to motion, so it is indifferent to waxing and waning.
The grounds for this conception are also manifold. To begin with, we find a perpetual confirmation of it in visual experience: we see the same object change its size as we move towards it or away from it; its shape, on the other hand, appears to us as sensibly invariant; accordingly, we view form as a permanent attribute of the object, and explain the change in magnitude as an illusion due to distance. Next there is the phenomenon of organic growth: to be sure, growth in magnitude is, as a rule, accompanied by change in form; yet this latter is so much slower [Pg 42]than growth that here too we are led to associate form with permanence, magnitude with change. It is interesting to speculate, what our geometry would have been like, if "growing pains" were a painful reality, instead of a mere figure of speech.
Last, but not least, come the psychological grounds for this conception. My memory records a series of disparate experiences which my consciousness associates with one and the same individual whom I call I. In spite of the many bodily and spiritual vicissitudes through which this individual has passed, my consciousness associates some permanence with him. I call this permanence my personality. This concept may be ever so incoherent and intangible, yet nothing can be more certain, for, this personality is undistinguishable from consciousness itself. Now, what I am about to say is not offered in any mystic spirit, but as a metaphor designed to illustrate a difficult thought. The thought is this: Man seeks an objective counterpart to this permanence which he calls his personality and finds it in form. Thus, in a sense, form is the personality of a geometrical being.
The logical independence of the fifth postulate from the other premises of Euclidean geometry suggests the existence of mathematical spaces neutral to displacement but not to expansion and contraction. What are such spaces like? We can get some insight by a comparative study of plane and spherical geometry.
Indeed, we can view the plane as a two-dimensional space, in which all the assumptions leading to congruence and similitude hold. On the other hand, with certain qualifications which are irrelevant here, those premises of Euclid which postulate congruence are valid on a spherical surface, on condition that we replace the term straight line by the term great circle. As a result, we can speak of spherical distances and angles, of spherical triangles and quadrangles; we can speak of displacement and of congruent figures; but we cannot speak of similar figures. Similitude is an exclusive attribute of the plane. On a spherical surface it is impossible to expand or contract a figure without either deforming it or destroying its contiguity with the surface. On a sphere free mobility is possible, free growth [F] is not; in a plane, both free mobility and free growth are possible.
[Pg 43]When we say that the plane is homogeneous and isotropic, we mean that there exist in the plane neither preferred points, nor preferred directions. In the absence of such absolute landmarks, we choose artificial ones, and any one such landmark is geometrically as good or as bad as any other. The same is true of the sphere; for, this relativity [R] is but a paraphrase of free mobility or of the "self-congruence" property which the sphere shares with the plane.
But a flat surface possesses also a relativistic property all its own; this property is a direct consequence of the attribute of free growth, and may be best brought out by again juxtaposing the plane and the sphere. On the sphere there exists a natural length in terms of which all other lengths may be measured: I am referring to the periphery of a great circle which may be viewed as absolute unit of length. Matters are different in the plane. It is impossible through the study of geometrical properties alone to detect the absolute magnitude of any plane figure, for the same geometrical properties are shared by an infinitude of other figures, similar to the one under consideration. In the plane, "great" and "small" have no more absolute significance than "fore" and "aft" or "here" and "there".
Euclidean geometry proscribes all speculations not only on absolute position, but on absolute magnitude as well. It is relativity with a vengeance.
To a species completely immobile there would be neither space nor geometry. In vain would he scan the objects which move past him: he would attribute the variations which these displacements cause to his senses not to changes in position, but to changes in state, since this being would have no means of distinguishing between these two sorts of change, and this distinction, which is of such capital importance to us, would have no meaning whatever to him.
Henri Poincaré, The Notion of Space
THE theme of this chapter is space-structure, more particularly, the structure of physical space. Only a century ago this last adjective would have been regarded as redundant, if not meaningless. Then there was but one space, and Euclid was its prophet; then space was a category, a form of human intuition, a synthetic judgment [S] a priori. Unlike those other ideas which the growing experience of the race could modify or invalidate, these synthetic judgments stood above and beyond human experience, enjoying a finality akin to that infallibility which in matters religious was bestowed upon Divine revelation.
There was no alternative: just as all breathed the same air, so all thought in terms of the same space. The psychological space of everyday life, the background of all man's efforts, conscious or unconscious; the physical space where the scientist conducted his observations and experiments; the geometrical space which the mathematicians peopled with their abstract configurations—were all but aspects of the same firm reality. For, like love in the Shakesperean sonnet,
[Pg 45]
. . . Space is not space Which alters when it alterations finds, Or bends with the remover to remove. O, no! It is an ever-fixed mark That looks on tempests and is never shaken. |
Well, many a reality of a yesteryear is today but a glaring indeterminacy. Is the space [S] concept an exception, or did it go the way of most realities?
Let us first consider the problem in retrospect. In the year 1733, there appeared a book written by one Gerolamo Saccheri [S], a Jesuit professor of mathematics and philosophy at the University of Pavia [P]. The title of the work was Euclides ab omni naevo vindicatus, i.e. "Euclid [E] cleared of all blemish." It was devoted entirely to the study of the Fifth Postulate, and, as the title indicates, the author believed that he had solved the ancient mystery. His reasoning was by reductio ad absurdum: he began by discarding the postulate and substituting for it alternative hypotheses, in the hope that such a course would eventually lead to consequences at variance with the other assumptions of Euclid. The results of his endeavors was a vast body of propositions which became the nucleus of what we call today non-Euclidean geometry [G].
In the Saccheri geometry, two parallels [P] may be drawn from a point to a line; similar figures do not exist; no triangle can possess an area greater than a certain definite magnitude; the sum of the angles of a triangle is always less than two right angles. Yet, "incredible" as these results were, Saccheri's endeavors to prove that they contradicted the other premises of geometry were not crowned with success, at least not in the eyes of other mathematicians. Still, his efforts were by no means fruitless. Just as Columbus discovered a new continent while in search of a route to an old land, so the attempts to prove an ancient assertion resulted in the erection of a new discipline of extraordinary fertility which was destined to change the scientific outlook on the universe.
Gauss [G] was the first to realize that all attempts to reduce the [Pg 46]Postulate of Parallels to the other axioms of geometry were foredoomed to failure, that the postulate was but a disguised definition of the plane, that its acceptance or refutation was not a matter of logical necessity, but was predicated by extra-logical considerations. But Gauss [G] was a wise man; recognizing that the time was not ripe for such revolutionary theories, he refrained from expressing his views in print, contenting himself with encouraging others. And so it happened that the credit for proving that the Postulate of Parallels [P] was indemonstrable goes to two mathematicians of a lesser lustre: the Russian, Lobachevsky [L], and the Hungarian, Bolyai [B]. While the two men had no contact—separated as they were by several thousand miles at a time when news generally, and scientific news particularly, traveled rather slowly—their contributions were strikingly similar.
The work of Lobachevsky and Bolyai appeared about 1830, but it was not until the sixties of the century—when the epoch-making dissertation of Riemann [R] entitled "On the hypotheses which lie at the Foundation of Geometry" was published—that the full significance of these contributions was recognized. About the same year, 1868, the Italian Beltrami [B] discovered the pseudo-sphere [P], a surface on which Saccheri's geometry was largely fulfilled. The term pseudo-sphere is not a happy one; pseudo-plane [P] would probably have been a more fitting designation, since, locally, at least, this pseudo-surface resembles the Euclidean plane. In fact, when a sufficiently small portion of the surface is considered, its pseudo-lines become indistinguishable from our own Euclidean lines. And yet, from a point of this surface two parallels may be drawn to any pseudo-line.
It was then that the remarkable analogies between plane and spherical geometries, which had already been known to the Greeks, began to be fully appreciated. For on the sphere [S] too, all the theorems of plane geometry which are independent of the postulate of parallels hold, on condition that the arcs of great circles, the geodetics [G] of the sphere, be regarded as equivalent to straight lines. This led to regarding any surface as the field of a special geometry of two dimensions. The geometry of Euclid thus had [Pg 47]become but a very particular kind in a vast aggregate of other geometries, each typified by a class of surfaces.
This brilliant conception was also due to Gauss [G], but it was left to his pupil Riemann [R] to amplify and extend these ideas to manifolds of any number of dimensions. We call such manifolds today spaces, mathematical spaces. Their variety is legion: they may be finite or infinite; bounded or boundless; of continuous or discontinuous structure; of any number of dimensions. Even when we confine our considerations to three-dimensional continuous spaces, we find their variety so great that the analogous problem of classifying surfaces—two-dimensional spaces we may call these latter—appears as child's play.
Which of these innumerable universes of discourse, if any, may be honored with the title physical space? Which, if any, conforms to the "true" universe as recorded by our scientific instruments?
Whatever might have been his classical predecessor's attitude on this question, the modern physicist is resolved to approach it without prejudice or favor. He would, no doubt, be delighted to learn that the assumption that physical space was Euclidean agreed with the experimental evidence at hand. For, of all possible hypotheses, this is certainly the most "desirable": it conforms best to the physicist's intuitive ideas; it is supported without reservation by the whole structure of classical geometry; and last, but by no means least, it is susceptible of the most elementary mathematical treatment.
However, the history of his science has taught him that simplicity [S] is an elusive term, that while a certain mathematical apparatus may appear the most simple in dealing with an individual phenomenon, its adoption may prove to be a formidable obstacle in the way of a unified science.
Besides, are not such appeals to simplicity wish-fulfillments rather than arguments? It is one thing to postulate that the universe is accessible to human reason; it is quite another thing to assert that it has been so designed as to be accessible to the mentality of a sophomore. No! Simplicity is no criterion of truth; neither is mathematical "elegance": in matters scientific, observation [Pg 48]and experiment are the sole arbiters of judgment. Do you remember the song of bygone years: "She don't have to look like a picture in a book, if but a good cook she should be"?
Now, physical space is three-dimensional, and the traditional approach to three-dimensional geometry is through the geometry of two dimensions. So let us proceed by analogy.
One feature which differentiates the plane from other surfaces is that it is self-congruent. What do I mean by self-congruence [S]? Well, imagine that, having made a plaster cast of some part of your body, say, of the muscle of your arm, you tried to apply this rigid form to any other part of your body; you would find it impossible to fit the cast "snugly" without distorting the body. If, on the other hand, the same experiment were made on a plane surface, it would be found that a templet made to fit one portion of the plane would fit any other portion. I express these facts by saying that the surface of our body is not self-congruent, while the plane is self-congruent.
It is this self-congruence of the plane that we utilize in reducing the general problem of congruence to that of triangles; also, in reducing further the congruence of triangles to that of segments and angles. It would seem, therefore, that the scheme which we have devised should be valid for the plane exclusively. Such, however, is not the case.
Indeed, while it is true that the plane is a self-congruent surface, it is not the only surface so distinguished. The sphere too has this property, that a rigid [R]templet which fits snugly one portion of its surface would fit as snugly any other portion. Furthermore, with certain reservations which do not concern us here, the same holds true for the pseudo-spheres of Beltrami which I mentioned earlier in the chapter.
To characterize the plane, we must seek some property which it shares with no other self-congruent surface. This brings us to another assumption implicitly contained in the Euclidean premises: a plane is a self-congruent surface such that a straight line passing through any two of its points is wholly contained within it. This property is characteristic of the plane, for neither the sphere, nor the pseudo-sphere [P] can contain a single straight [Pg 49]line. It remains, therefore, to find an unequivocal definition of the straight line.
"Straight [S]," says Euclid, "is the line which lies evenly with any of its parts." When we interpret this statement in the light of the subsequent use made of it by Euclid, we come to the conclusion that what Euclid meant was that any rigid templet which fits one portion of a straight line would fit any other. In other words, what seems to distinguish the straight line from any other one-dimensional form is its self-congruence.
But, obviously this definition is not characteristic of the straight line. A circle [C] too is a self-congruent form, for it too "lies evenly with any of its parts," since a rigid templet which fits snugly any portion of the circle will fit as snugly any other. The same is true of the so-called helix: the outline of a screw may serve as an illustration of this last line. How are we to distinguish the straight line from such other one-dimensional forms?
Shall we say that what marks the straight line is the fact that if two of its points lie in a plane all its points lie in the same plane? Obviously, we would be in a vicious circle: one cannot define the plane by means of straight lines, then turn around and formulate the lines in terms of the plane!
How about the fact that one and only one straight line may be drawn through any two points of the plane? Is not this a characteristic property, valid exclusively for the straight line? No. On a sphere too there exists a system of self-congruent lines such that through any two generic points passes one and only one line of the system: I am referring to the so-called great circles. To be sure the analogy between the great circles on a sphere and the straight lines in the plane is subject to two important reservations: in the first place, any two great circles meet in two diametrically opposite points of the sphere, and not in one point, as do two straight lines in a plane; in the second place, through any two diametrically opposite points of the sphere pass not one, but any number of great circles. However, a closer analysis will reveal that for the concrete problem at [Pg 50]hand these reservations are not as clear-cut as they may at first appear.
Indeed, the concrete problem with which the physicist is concerned does not involve a plane extending indefinitely in all directions, nor the total surface of a sphere, but rather a finite bounded area. Before me is a plaster cast of a surface: by means of a small rigid templet I have ascertained that the surface is self-congruent; I at once eliminate the possibility of the surface being pseudo-spherical, for the latter is not convex; it remains, therefore, to ascertain whether it is spherical or flat.
With this in view, I stretch along the surface a cord; pull it until taut and trace its outline on the surface; by means of a rigid templet, I have satisfied myself that the line thus obtained is self-congruent. I now argue that the line is either straight, or it is in the form of a circular arc; if it be straight, the surface is flat, if it be circular, the surface is spherical. Which is it?
All the finite attributes which Euclid ascribes to the straight line avail me nothing, for they apply equally to arcs of great circles on a sphere. Through two points passes but one such taut string in either case; two such taut strings, if they meet at all, meet in but one point in either case. To be sure, were it possible to extend the surface indefinitely, the question could be settled readily enough: the circle is a closed form, while the straight line can be continued indefinitely in either direction without ever retracing one's steps. But while we are in the habit of invoking such extrapolation [E] on every hand, from the purely physical standpoint it has no greater value than a prayer, for we have no concrete means for executing such an indefinite extension.
Nor can we hope to derive an answer to our question from the numerous consequences of those Euclidean assumptions which precede the postulate of parallels; such, for example, as congruent figures, or perpendicular straight lines. For, all these theories of plane geometry have their spherical counterparts.
Now, the problem of determining the structure of physical space is not essentially different from that of determining the [Pg 51]character of a surface. In either case one must be in possession of a rigid templet and a rigid standard of length. Both functions may be performed by one and the same instrument, say by a rigid rod; details of design do not concern us here; of one thing we must be certain beyond all peradventure: the instrument must be absolutely rigid.
We inquire next: How is one to ascertain whether a given object is rigid or not? And no sooner do we ask this question than we realize that we have landed in one of those logical traps which are so characteristic of problems touching on the foundations of physics. For, in the last analysis, testing means comparing with standards. Hence, whether an object is rigid or not, may only be decided by juxtaposing it with some other object the absolute rigidity of which is certain, and we know of no such objects.
What is the alternative? Well, in the absence of absolute standards one accepts standards on which universal agreement can be reached, and this, precisely, is the solution of the problem of rigidity which man has unconsciously accepted since time immemorial. We have no quarrel with such a solution, provided it be adopted in the full realization of its implications; what it implies is that we abandon the concept of absolute rigidity in its entirety and declare certain accessible objects of our environment rigid by fiat. Henceforth it will be meaningless to assert that such and such an object, say A, is rigid, unless we concede that such a statement is just an elliptic expression for such other statements as object B is as rigid as object A; or if A is rigid, then B too is rigid.
Some readers will, no doubt, object to the term by fiat applied to such ideas as rigidity; they will counter that obviously the choice of such standards is not arbitrary; that many objects in our environment would be excluded a priori, while among those eligible some would certainly appeal to all sound people better adapted as standards of rigidity than others. Let us examine the matter closer.
. . . Experience [E] played an indispensable role in the genesis of geometry; but it would be a mistake to conclude from this that geometry is an experimental science, even in part. If it was experimental, it would be but approximate and provisional. And what a crude approximation! . . . Experience guides us in the choice of the standards which it does not impose on us; experience does not tell us which geometry is true, it tells us which is the most convenient. Observe that I was able to describe above the fantastic worlds which I imagined without ceasing to use the language of ordinary geometry.
Henri Poincaré, Space and Geometry
THAT we are guided in our choice of standard by some criterion of rigidity [R] common to all sound people is beyond question. Consider, indeed, an individual who had earnestly proposed to use a column of mercury enclosed in a glass tube as a device for measuring lengths. If he persisted long enough he would end by landing in the happy refuge of all contemporary Caesars and Napoleons. Why would his scheme appear to us so preposterous? Well, were his method universally adopted, strange results would follow: having measured a certain lot on a summer day and found it to be 50 feet wide, we would, upon repeating the measurement on a winter day, find that the width had grown to 60 feet; for, the column of mercury having contracted with the drop in temperature, the second measurement would be performed with a smaller unit. There would be a rush by real estate owners to sell their lots in winter, and purchasers to buy them in summer. Similarly, the numbers which represent the heights of our buildings, the lengths of our railroads, in fact, any length, area, or volume would shrink and swell with the seasons; nay, from day to day and from hour to hour.
[Pg 53]"But," would our hypothetical innovator counter, "how do you know that mercury expands with heat? I, for one, emphatically hold that mercury is the one material which is geometrically permanent. Therefore, my mercury scale indicates the true state of affairs, while your notion that buildings, roads, tables, chairs, and instruments are permanent is but a grievous illusion. They contract with heat and expand with cold, just as does this glass tube which contains the mercury." Well, how can we cope with one who holds forth such ideas? Not by logical arguments, of course, but by putting him away as soon as possible where he cannot disturb practical men.
Still, moved by an unaccountable curiosity, we resolve to interview the iconoclast in his cell. He has had ample leisure, and this has caused him to amplify his ideas. He has discovered a new and original criterion of straightness [S]. We find him holding between his hands a thin flexible rubber hose. This, he tells us, is the templet by which one may ascertain whether any line is straight or curved. We point out to him that his flexible instrument is wholly inadequate for this purpose, inasmuch as it bends and twists, even while he holds it in his hands. To this he replies that we are mistaken; we rely altogether too much on hearsay and authority; this circumstance he traces to wrong education and training, which have obscured from us the real world and replaced it by illusions.
He adds that he too had been so handicapped. But through perseverance and contemplation he has succeeded in shaking off such prejudices. He knows now that his rubber hose is the one permanent form in the universe, the one model of that straight line which geometers of all times have vainly attempted to define or describe.
To prove his point, he proceeds to apply his method to testing the straightness of objects in his cell. He places his hands above the two corners of a table, holding his hose between them. "Well," he exclaims, "confess that you have hitherto regarded the edge of this table as reasonably straight. Now, however, after having beheld the ideal standard of straightness, you must realize that the edge is really curved, inasmuch as it departs [Pg 54]to a considerable degree from this standard. Besides," he continues, as the hose keeps swaying and squirming between his nervously shaking fingers, "this should cure you of still another of your prejudices. When you compare this edge with the perfect model of rigidity which I hold between my hands, you clearly see that this table, which you have been in the habit of thoughtlessly considering as permanent in form, is in reality a swaying and squirming mass."
We leave him with a mixed feeling of satisfaction and perplexity. It certainly is a comfort to know that men like this are not at large. Still, we realize that it is one thing to convince an alienist, quite another to have one's arguments sustained in a court of physical inquiry.
Free mobility [F] and free growth [F], such are the principles which underlie our intuitive notions of space. Do these two principles suffice to characterize space? From the mathematical point of view, yes, because these assumptions lead to flatspace and flatspace only. From the physical standpoint, no, for, one can conceive a great variety of physical universes which satisfy these requirements. In the following pages is exhibited one of these universes [P], the modification of an idea of Poincaré.
This would-be universe is peopled with beings of our own type of intelligence who observe and speculate, even as we do; who use our own principles of logic, and who, as a consequence, have developed a mathematics along our own lines.
Their universe is bounded by a spherical surface; the interior of the sphere is filled with a fluid, in which these hypothetical beings can move about freely in all directions.
From our point of view, their world has a number of peculiarities which, however, are all "within reason." Thus, unlike the case of our own world, the temperature at any point of the universe is not subject to variation with time. It does vary, however, with the distance of the point from the center, diminishing continuously as one travels towards the periphery; hence, the climate is hottest at the center, coldest on the boundary; and, since the temperature depends only on the distance [Pg 55]from the center, it is one and the same at all points on any sphere concentric to the boundary of that universe.
Another peculiarity of that would-be world is that, while the variety of materials to be found therein is as great as that of our own, all these materials have the same coefficient of expansion; i.e. the fluid medium, all rigid bodies, the bodies of the observers themselves, all their scientific instruments and tools—in fact, their entire environment—expand at the same rate with the increase in temperature, and contract at the same rate when the temperature drops.
Were we to peep into their universe, all geometrical magnitudes of a body would appear to our eyes as changing when this body is being displaced from the center towards the periphery; not, however, to the beings who inhabit it, for there is nothing in their environment by means of which they could detect such changes.
What sort of geometry would these beings devise? What sort of ideas would they form concerning lines, planes, or space?
Would these beings conceive their world as finite, or as infinite? This would depend upon the actual law which controls the variation of the temperature with the distance from the center. It is obvious enough that there is an infinite number of mathematical laws which would satisfy the conditions we have thus far stipulated. We shall select this law in such a way that their universe would be conceived as infinite to these beings, even though to our eyes the sphere may not appear greater than one meter in diameter.
Imagine, indeed, that these people, who originally congregated in the warmest region near the center of their universe, have been compelled, as they fructified and multiplied, to move further and further peripheryward. As they do, their chattels, their vehicles, their instruments, even their bodies contract. If an ambitious explorer among them would undertake a voyage towards the furthermost regions, his movement would appear to us as becoming slower and slower. However, he would rightly maintain that he is moving at a uniform [U] rate, since his instruments indicate that he is covering equal distances in equal intervals of [Pg 56]time. And it is obvious enough that if the temperatures, and therefore the contraction, diminish as the distance from the center becomes greater, the explorer would never reach the periphery, however fast his speed may appear to him. He would, therefore, reach the conclusion that his universe is infinite in that direction.
But the same would be true of any other direction; for, while the center of their universe and its radii would appear to us as of special significance, these beings would make no such distinction. All points would appear to them equivalent, and so would all lines. Thus their space which we regard as finite, heterogeneous, and anisotropic, would appear to them as infinite, homogeneous [H], and isotropic, just as ours appears to us.
Should these beings construct a railroad leading, say, from the center towards the periphery, they would—using our own engineering principles—lay down two tracks at a constant distance from each other. This railroad would appear to us as two lines converging towards the periphery of the sphere; not to their senses, however, for they would regard the rails as parallel. Nor would the situation change if the railroad track was laid along a non-radial line; for, as I said before, they make no such distinctions. And so, on the basis of their experience, they would be led to postulate that two lines which remain at a constant distance from each other did not intersect, no matter how far continued. In other words, they too would be led to the Euclidean theory of parallels [P], and, by using arguments identical with our own they, too, would conclude that their space was flat.
In fact, were our communications with those beings limited to an exchange of geometrical knowledge, we could never become aware that their world differs in any way from our own. It is only when we attempt to impose on them our own standards of rigidity that the essential peculiarities of their world would become apparent to us. Particularly would this be true of the straight and the round.
What we conceive as a rigid straightedge made of our own material (which, unlike the materials of that strange world, is not subject to appreciable changes with temperature) would play a very insignificant part in the geometry of those beings, inasmuch [Pg 57]as the mathematical equation which they would assign to it would be rather involved, and its physical applications next to nil. Such a standard would not represent the shortest distance between two points, even though in measuring lengths those beings did proceed as we do; i.e. taking a standard rigid rod as unit, they would determine the number of times it will fit a given path, and declare this number to be the measure of length of the path. Conversely, the unit rod which they would regard as permanent would to our eyes change with temperature; i.e. with the distance from the center, of their sphere.
Consider, indeed, two points at equal distances from the center of that universe. Having procured a number of cords of various lengths, one of the physicists of this would-be world would place them between these points. He would find some too short, some too long; one of these cords would, however, appear to him as taut; the position occupied by this latter he would declare to be the shortest distance between the two points. That the form of this line would not meet our specifications for straightness may be seen from the following considerations: let us take their world into our laboratory and bring all points to the same temperature; stretch a cord made of their material between these two points; the subtended cord assumes the form of the "human" straight line. Now, let us restore the temperature-expansion distribution which prevails in their world. Then, since the middle of the cord is now closer to the center than are its extremities, the cord must expand; while to us the new form appears slack and curved, for them it would now occupy the shortest path. If, then, they too would call their geodesics [G] straight lines, they would come to the conclusion that they might use the taut cord as a criterion of straightness, just as we do.
Nor would we fare better with our other criteria of straightness. Suppose that this hypothetical physicist had prepared a rigid rod designed according to our "human" ideas of straightness, but made of the material prevalent in his own universe. Holding the extremities of the rod fixed, he revolves it. He finds that unless the ends are placed in special positions, the rod will not appear stationary when revolved. On the other hand, should he give his [Pg 58]rod the shape of a geodesic of his own space, all points of his rod would appear to him as immobile; for, an axis of revolution in that strange world would not have the form of a "human" straight line, but that of a geodesic.
The same geodesics might serve as the paths of light-rays. For, because of the variable contraction, the fluid medium would have a variable density and, consequently, a variable index of refraction [R]. Light in that universe would, therefore, travel not along straight lines, as we conceive it, but along curved paths. Now it would be possible to select the distributions of temperatures and the law of expansion of the material in such a manner that these curved paths would be identical with the geodesics; i. e. with the shortest paths of their space.
To be sure these geodesics would appear to us as complicated curves. Yet, formally, they would be fully equivalent to our straight lines, for they would satisfy in that universe all criteria by which we test straightness in our own: these curves would be the configurations assumed by taut cords; they would be the shortest distances between points; they would serve as axes of rotation; they would serve as trajectories of light. Moreover, in the analytic geometry of those beings these geodesics would be represented by the most simple equations, the linear, because their reference system is made up of those very curves.
In vain would we attempt to convince those beings that they were laboring under a gross illusion; we could not suggest to them a single experiment which would make them physically aware of the "actual" state of things. Every geometrical concept we possess they could match by an equivalent concept; to every logical mathematical consequence that we derive from our own concepts there would correspond in their conceptual scheme an equivalent result; and just as the consequences which we draw from our own geometrical laws are verified by our own experience, so would the analogous consequences drawn by these would-be people be substantiated by theirs.
Formally, their geometry would be fully equivalent to our own. If they have not produced their own Euclid [E], they could use a translation of ours. Even the figures accompanying our own [Pg 59]texts on geometry could be utilized without modification, provided they be traced on their "paper," since the instant these figures would reach their universe, the sheets on which they were drawn would automatically curve into pseudo-planes, the circles [C] into the pseudo-circles, etc. . . .
Complete and harmonious co-operation could be established between the mathematical societies of the two worlds. We could engage their geometers for the solutions of our problems, and reciprocate the service. For, all our mathematical and geometrical criteria would be identical, and it is only in "physical content" that the two geometries would differ.
Nothing that those beings could do, nothing that they could observe, test, or calculate pertaining to the geometrical properties of material bodies in their environment could reveal to them that their world is not what they believe it to be.
Can our own geometrical experience, tests, observations, and calculations reveal to us whether our geometrical universe is what we believe it to be? Imagine that there exists in our world some influence that affects in a uniform manner all the geometrical properties of material objects in our environment, including our own bodies; grant, further, that we are physiologically incapable of perceiving this influence, just as those fantastic beings remain insensitive to expansion and contraction due to changes in temperature. Nothing in our physical experience could then reveal to us this influence, and the geometry which we would develop under such circumstances would in no way differ from our present geometry.
As a matter of fact, overnight such an influence may have arisen, or it might have been operating since the beginning of time, without our being aware of it, no more than we are aware of the intricate motion of our earth in space. Our bodies and our dwellings, our tools and our instruments, our landscapes and our heavens may be squirming and deforming in the weirdest conceivable fashion—as long as they deform in unison with each other and with us, we would not be cognizant of the event.
Is this straightedge truly straight? Is this disc truly round? [Pg 60]This table truly plane [P]? Or are all these notions illusions which prey on our senses? An observer who would himself be immobile and rigid in the absolute sense of these terms could answer these questions: for, by observing the manner in which a body deforms as it passes through a given point of absolute space, he could—were he but a geometer—determine the actual structure of space.
But is not such a god-like observer just a symbol of what man is not, and what, in the nature of things, he shall never be? Might we not as well relegate the problem of space-structure to the vast store of other questions which we classify as unknowable? No! Such resignation would be premature. All one may legitimately conclude from the preceding analysis is that geometry alone will not solve the problem. But geometry is only a small part of our knowledge.
The physical reality [R] that impinges on our senses is like a rapidly unreeling moving picture film, whilst the world as it appears to the geometer is like the individual images obtained by stopping the film at convenient instants. Could one determine the mechanism of a cinematograph by just examining a few of the pictures that make up the film? Well, no more should one expect to derive the structure of physical space from the static considerations of position and form of the bodies in our environment.
There is the vast interplay of forces which bring about the motion of these bodies; there is the intimate interaction of the molecules of which those bodies are made up, and of the atoms which make up these molecules; there is, above all, that other categorical imperative, time [T], the essence of all phenomena, which the geometer so conveniently eliminates from his considerations. Here, perhaps, we may find the clue to the mystery which the geometer is admittedly unable to unravel.
Before a complex of sensations becomes a recollection placeable in time, it has ceased to be actual. We must lose our awareness of its infinite complexity, or else it is still actual . . . It is only after a memory [M] has lost all life that it can be classed in time, just as only desiccated flowers find their way into the herbarium of a botanist.
Henri Poincaré, On Measuring Time
"ABSOLUTE true and mathematical time," says Newton in the Scholium of Principia already quoted, "of itself and its own nature flows equably without regard to anything external, and by another name is called duration [D]."
Today the term equable sounds archaic: we say uniform [U] instead. A variable magnitude is said to change uniformly if it grows or dwindles at a constant rate. And what is rate? It is the change that occurs in a unit of time. And how do we establish such a unit? We choose some uniform change for standard: the unit of time is then, by definition, the interval required to bring about this standard change.
Recognizing the circular character of this definition of uniformity, Newton distinguished between time in the vulgar sense of the word and mathematical time, or duration, which he conceived as flowing uniformly on a priori grounds. The average man fails to grasp this subtle distinction; he accepts the absolute uniformity of time as a sort of axiom, conceiving his own consciousness as flowing in perfect synchrony with duration.
And yet, our awareness of existence is stimulated not by the continuous, but by the intermittent phenomena in our environment. The pragmatic form of time is not flow, but rhythm [R]. The words "life is rhythm" are more than rhetoric. Nor does this sense of rhythm which we all seem to possess call for occult explanations [Pg 62]inasmuch as most of our vital processes are periodic phenomena. It will be sufficient to mention the action of the heart, the pulse, breathing, locomotion, alimentation, fatigue. That we unconsciously respond to these incessant and recurrent physiological fluctuations, synchronizing our impressions of the external world with these inner cycles, is as plausible an hypothesis as any offered to explain our sense of rhythm.
To be sure, not all vital phenomena are recurrent. Individual life is aperiodic: a man is born but once, he will die but once. But viewed from the standpoint of the race, birth, growth, decay, and death do form a veritable cycle; and the many theories of transmigration and reincarnation which have held sway over the soul of man bear witness to the immanence of this conception of eternal return.
In the world without us, too, the periodic phenomena [P] are both abundant and striking. Day and night, the changing shadows; the lunar cycles, the tides; the seasons, the variable flora, the annual floods in the river valleys, the recurring positions of the stars—such are some of the time-keeping devices imposed as it were upon man by nature.
The periods of these natural phenomena are beyond the control of man, and so he has sought in his environment phenomena of a controllable character that could be utilized for the purpose. Among the great variety of such recording schemes known even to the ancients are: the sun-dial; the water-clock, which works on the principle that water emerging through a small aperture drips periodically; the sand-glass, which utilizes the sensible regularity in the flow of fine sand; the pendulum clock, which harnesses the oscillations executed by a weight suspended in a vertical plane.
Now, theoretically, any recurrent phenomenon, whether astronomical, physical, or physiological, or any convenient mechanism designed to run in synchrony [S] with such a phenomenon, could be regarded as a clock. Theoretically, the period of any such mechanism could be taken for unit of time. Yet not all such devices would possess in our eyes the same degree of dependability. No normal man would regard pangs of hunger as a reliable [Pg 63]indication of time; he would, probably, put greater faith in some device synchronized with his pulse; still he would hardly regard even this as a satisfactory solution of the problem.
The man in the street, confronted with the task of selecting, from among the many recurrent phenomena in nature a universal timekeeper, would proceed by elimination. Certain recurring phenomena he would reject unqualifyingly as wholly undependable; others he would endeavor to classify according to their regularity. If asked what he meant by regular, he would answer that a clock [C] is regular if any two successive time-intervals recorded by it are congruent [T]. If pressed further to specify some test by which one could ascertain whether two such time-intervals are or are not congruent, he would have to admit his helplessness. And yet, he had acted all his life as though he possessed some instinctive criteria of uniformity, as though there were stored in the innermost recesses of his consciousness a master-clock which ticked in perfect synchrony with duration. If only there were a way of translating these hazy instinctive notions into actual physical data!
The problem bears a remarkable resemblance to the one we encounter while studying the measurement of length. There we are led to stipulate the existence of a measuring rod unalterable in length. In short, we demand of our standard rigidity, and it is, indeed, a species of "temporal rigidity" that we demand of the periodic devices which would serve as standard timekeeper.
Let us pursue this analogy for a while. The scientific unit of length, the meter [M], is a metal rod on deposit at the Bureau of Longitudes in Paris, and kept there under as constant conditions as human ingenuity can devise. Despite this meticulous care, the scientist regards the meter as a relative standard. To be sure, it did not begin its career in this humble capacity. The savants of the French Revolution [F] who inaugurated the metric system of measurements naturally wanted their basic unit to be as permanent as the fruits of the political system to which it served as a complement. Nothing short of the circumference of the earth would stand such an acid test; accordingly, one ten-millionth part of a quadrant of the Parisian meridian [M] became the official unit of [Pg 64]length. Alas! Much has changed since those balmy days, including the Parisian meridian [M]. The meter [M] survived, reduced, however, to the rank of a mere metal stick in a glass case.
We know today that geometrical rigidity [R] in the absolute sense is unattainable; that relative rigidity is the most one can reasonably expect of a measuring device; that such criteria of congruence as are available go no further than testing whether certain proportions remain permanent; that we have no means at our disposal of detecting absolute changes in length; that changes in length which affect in unison all the objects in our environment are as inaccessible to our scientific instruments as they are to our senses. Is it otherwise with time? Is it possible to construct an absolute clock, devise an absolute unit of time, establish criteria of absolute time-congruence [T]?
The problem is to find a periodic phenomenon which would possess that perfect uniformity [U] which we ascribe to duration. The discovery of such phenomenon would bestow upon the term uniform physical significance. The utilization of the phenomenon for the construction of a master-clock would then be a mere matter of technical detail; since the period of the phenomenon would be permanent beyond peradventure, it could be taken as absolute unit of time; henceforth, the question of whether a certain change did or did not occur uniformly would be decided by the simple expedient of comparing its fluctuations with those of the phenomenon chosen as standard.
We commence by examining the scientific technic used in measuring time. The scientific unit of time, as we all know, is the second. This is 1/86,400-th part of a day. What day? The question is pertinent, for there are several. Is it the solar day, i.e. the time of a single passage of the sun from zenith [Z] to zenith? No; our experience tells us that this period is sadly variable, not only with the seasons, but from day to day. Then perhaps it is the mean solar day [S], which is obtained by dividing the year into 365.24 219 879 parts? No: this, we are told, is a purely formal magnitude and would afford no check on uniformity.
It is on the so-called sidereal day that has been bestowed the function of timekeeper-in-chief. The sidereal day [S] is, by definition, [Pg 65]the interval of time consumed in a single revolution of the earth; or, if you prefer, the time which it takes some "fixed" star to return to a definite position with respect to a "fixed" post of observation, say to the hairline of a telescope singled out for its precision. The sidereal day, astronomers tell us, exhibits a most remarkable uniformity. What precisely do they mean by this statement?
The division of a sidereal day into 86,400 seconds is effected by means of precision clocks. For example, the observatory of Paris has four such clocks, placed a hundred odd feet under ground to assure constant temperature. Each clock is encased in a hermetic enclosure, where the atmospheric pressure is held constant; to protect the clocks from the disturbing influence of man, all access to these subterranean cells is barred, the winding, adjusting, recording being effected by means of electrical transmission from the observatory. The precision thus attained leaves little to be desired, and what little individual discrepancy does occur in any one of the four clocks is immediately detected by checking it against its companions.
The construction technic of these precision clocks has made enormous strides since the days of Galileo and Huyghens, the creators of chronometry; and it may indeed be said that the only thing about such time-pieces which has not changed since those early days is gravity, for the pendulum [P] is still the principle on which these ultra-modern clocks operate. We have all learned in school that a pendulum suspended in a vertical plane when slightly displaced from it position of equilibrium will execute oscillations of a constant period. The actual value of the period, we were taught, depended on the length of the pendulum, on the acceleration of gravity, and on the resistance of the medium. According to the laws of classical physics, the oscillations of a pendulum are congruent to each other, provided the conditions just outlined remain reasonably constant.
Thus, in the case of the observatory clocks described above, constant temperature should guarantee the invariable lengths of these pendula; with atmospheric temperature maintained constant, the resistance of the air to their motion should not vary; [Pg 66]as to the gravitational acceleration, it is assumed constant for any given location. Theoretically, therefore, the oscillations of any one of these precise instruments should be as nearly congruent as is humanly attainable. How is one to check this uniformity experimentally?
We are answered that innumerable observations have proved that there is a remarkable agreement between the period of a complete revolution of the celestial sphere and the daily number of oscillations of any one of these mechanical time-pieces. This means, by extrapolation, that if one of these clocks was adjusted to beat out exactly 86,400 seconds on a certain sidereal day, it will continue to do so on all successive days, and for ever more. From which we may conclude that a certain pendulum executes exactly 86,400 oscillations every time the celestial sphere returns to a certain position relative to the observing post. Can we conclude, however, that all these oscillations are congruent to each other, or that all sidereal days are of equal length? Obviously, not!
To be sure, if we did know that the oscillations of the pendulum were all congruent to each other, day in day out, we could conclude therefrom that the rate of the rotation of the earth too was a constant. But we have no such assurance; or, at least, not one of a verifiable character. Of course it may be argued: "It stands to reason that the oscillations of these precise clocks are congruent to each other, for how otherwise could one account for the fact that it is possible to maintain indefinitely a battery of such clocks in nearly perfect synchrony? If, indeed, there existed a disturbing cause capable of upsetting the uniformity of any one of these clocks, it would be of such a character as to affect simultaneously, and to the same degree, all these time-keeping devices; a highly improbable hypothesis!"
Arguments of this sort are quite frequently used in the sciences, when more adequate reasoning fails. They are based on a principle known as that of sufficient reason [S], which would, however, be more aptly described as that of insufficient reasoning. The principle of sufficient reason asserts that if one knows of no cause which would tend to render two entities different or unequal, [Pg 67]one may legitimately infer that they are identical or at least equal. The inadequacy of this argument in the case under consideration is too obvious to require comment.
Now, while the uniformity of the earth's diurnal motion [D] is susceptible of neither logical proof nor experimental verification, there is no reason why we could not, by universal agreement, bestow upon the sidereal day the function of official timekeeper, and use the diurnal rotations of the earth as criterion of relative uniformity for any temporal series. Henceforth, of course, no absolute significance would be attached to the term uniform: the assertion that such and such a phenomenon was uniform would be just an elliptic expression, the words relative to the diurnal motion of the earth being always implied.
Such a convention would be equivalent to declaring the diurnal motion of the earth uniform by fiat, but this would not disturb the modern physicist in the least. The classical physicist, however, who viewed such statements not as conventions but as assumptions, would feel quite uneasy about such a declaration, inasmuch as it stood in direct contradiction to Newtonian [N] Mechanics [M], according to which the diurnal motion of the earth could not be uniform unless the earth was free from all perturbations, external or internal. Now while the stars, the sun and the other planets of the solar system are too remote from the earth to cause much trouble, the same cannot be said of the moon. It is well known that the tides brought about by the motion of our satellite produce considerable friction, which, in turn, should cause periodic accelerations and retardations in the diurnal rotation. Furthermore, it has been surmised for some time that the terrestrial crust is subject to periodic variations in magnitude, a phenomenon picturesquely called "breathing," and that these fluctuations, too, must cause appreciable changes in the rate of the earth's motion. Thus, from the standpoint of classical mechanics, the diurnal rate cannot be regarded as absolutely constant.
What other phenomenon could be used in lieu of this rotation? We naturally turn to the precision clocks described above. Just as the scientific unit of length is the meter [M], a metal rod kept under constant conditions at the Bureau of Longitudes in Paris, [Pg 68]so could, by universal agreement, the second be defined as the interval of time which it takes a certain clock, say one of the four kept in the subterranean cell under the Parisian Observatory, to complete a full oscillation. Epistemologically, such a mechanical procedure is far superior to the astronomical; for at least it does not tend to conceal the relative nature of the selected unit of time. The relative constancy of the second becomes then as evident as the relative constancy of the meter.
As a datum of experience time is a meager thing. What an individual can say about his experience with time constitutes his autobiography. Unadorned, such an autobiography is just a chronology of disparate events based on vague recollections: it is the imagery of words that brings these misty memories out into sharper relief.
Our awareness of existence, for which consciousness is another name, is stimulated by shocks. When violent and rare, these shocks remain engraved on our memory; when mild and frequent, they create in us the sensation of rhythm. But violent or mild, rare or frequent, shocks are our only means of recording experience, and we know of no other method for measuring time than by counting shocks.
Duration [D], the sublimated time which our mind has fashioned from this raw material, is quite another thing. Interpolated between any two experiences and extrapolated beyond all experience, it is continuous and eternal. The prototype of all that is uniform and steady, duration is conceived by us not only as flowing in synchrony with our consciousness but as carrying the whole universe in its flow.
If every point in the universe were provided with a clock, and if all clocks were set alike, synchronized with duration and released at the same instant, then at any future instant, however remote, these clocks would all indicate the same time, cosmic time, absolute time. Thus speaks the untutored mind, and what mind was not untutored in this regard before the advent of the modern theory of relativity? Indeed, the untutored mind conceives duration as wholly independent of the post of observation, [Pg 69]or of the event recorded. It conceives any one of the hypothetical clocks just mentioned as ticking in absolute synchrony with any other of these clocks, and this regardless of whether the point in space, to which this clock is attached, be vacant or occupied by matter, regardless of whether the present incumbent of the point be at rest, be engaged in continuous motion, or be in the throes of a cataclysm.
Why is this belief in the universal character of time so firmly rooted in our mind? Because we conceive that by a mere act of the mind we can transfer ourselves to any point in the universe. This act we conceive as effortless and instantaneous, as though an invisible rod connected our position to that hypothetical point, a rod so perfectly rigid that no time is consumed in effecting the transit.
Nor is our imagination constrained to remain at any one point at any given instant. A material body may not occupy two positions at the same time, but we will not or cannot apply such restrictions to our mind, which not only may be anywhere at any time, but everywhere at all times. It is indeed this alleged omnipresence of our mind that makes geometry at all possible as a physical science; for, geometry is the study of a world from which time has been temporarily abstracted. We act as though the universe were a moving film, the operator of which would obligingly at our mere request stop the mechanism at any convenient instant, so that we may examine the picture in detail.
We may recall here Zeno's [Z] celebrated paradox, "The Arrow." "Whatever moves," argued the Sophist, "is moving in the now; but whatever is in the now is motionless; hence the moving arrow is at rest." Like the arrow of Zeno, so was the universe of classical physics: in continuous flow, and yet immobile at any given instant. This duality, moreover, was construed by the classical physicist as a pragmatic necessity, and the great d'Alembert went so far as to erect it into a fundamental principle of mechanics, a principle which to this day bears his name.
According to that principle, any moving system could be regarded as a system in instantaneous equilibrium [E]. How? Through [Pg 70]the simple expedient of replacing the movement by a fictitious static force [F] called inertia [I]. The principle reduced any problem in dynamics [D] to one in statics [S]: by freezing a moving system and keeping it in storage for as long as he pleased, the classical physicist could study at his leisure not only the geometry of the system, but its mechanical details as well.
We possess no direct intuition of simultaneity [S], nor of congruence between time-intervals . . . We supplant these intuitions by rules which we almost invariably apply without giving ourselves account of them . . . We chose these rules not because they are true, but because they are the most convenient. We may sum up these rules by saying: the simultaneity of two events or the order of their succession, and the equality of two time-intervals must be so defined as to make the statement of natural laws as simple as possible. In other words, all these rules, all these definitions are but fruits of an unconscious opportunism.
Henri Poincaré, On Measuring Time
IT HAS been remarked by more than one contemporary writer that Newton occupied the same position with respect to classical science as does Einstein with respect to modern. While this may be true in some respects, these writers fail to bring out one very important difference. The notions which Einstein introduced into physics are repugnant to the intellect of a normal man; while Newton, in positing his concepts of absolute space and time [T], was merely following the dictum of that "inner voice" which incessantly whispers to all of us that space is a permanent stage on which events are unrolling in perfect synchrony with our stream of consciousness. Of all conceptions which I have thus far examined, the cosmic character of duration [D] and the closely allied idea of causation [C] are most firmly rooted in the human mind. They were also the last ramparts of physical "absolutism" to yield to modern critique.
The point of departure of that critique was the problem of simultaneity [T]. What do we mean by simultaneous events? What concrete means has the physicist at his disposal to ascertain whether two events have occurred at the same time or at different times? The problem is of paramount importance; indeed any [Pg 72]situation where time is at all a factor is, in the last analysis, reducible to a question of simultaneity. Certainly, one who would speak with any degree of confidence of cosmic time [C] should at least be able to explain what he meant by the same time.
We are not concerned here with the case when the two events are apprehended directly by the same observer's senses, since the simultaneity of two such perceptions is a judgment that derives its validity from our ability to respond simultaneously to two or more stimuli. Inasmuch as this faculty is the genesis of all experience, and of all judgment too, it is not a subject for critical analysis. One who doubts the validity of such judgments doubts the possibility of knowledge; and while such doubts are as valid as any other, one who sincerely entertains them cannot consistently engage in any discourse.
Thus whether two perceptions sensed by the same individual are simultaneous, and, if not, which of the two precedes [P] the other are judgments the validity of which is irrefutable, and on a priori grounds. What is more, whether we like it or not, all empirical reasoning consists in reducing alleged facts to just such primary judgments as to a last court of appeal. The fear that our senses may deceive us casts doubts on all perceptual judgment; the only apparent way out of this dilemma is to check our own perceptions against the perceptions of those whom we consider our peers in judgment. The more of these peers subscribe to our judgment the more reliable the latter appears to us. The question as to whether there is more to objective truth [R] than mere collective agreement must remain unanswered, inasmuch as we have no other criterion for objective truth than collective agreement.
These general considerations have an important bearing on the problem of time. Have such and such two events occurred at the same time or at different times? Ultimately, the answer to any such query will depend on the temporal order of some two perceptions sensed by some individual, reinforced by similar reactions of other individuals.
Now, long before the advent of the modern relativity [R] theory, [Pg 73]it was generally recognized by physicists, and not only by physicists, that the temporal order of two events as well as simultaneity were relative notions. A few examples will suffice to bring this out.
You see lightning burst forth, and a few seconds later you hear the rumblings of thunder. Despite the interval elapsed, you ascribe the two phenomena to the same electric disturbance. You argue that in the immediate vicinity of that disturbance you would have perceived the light and the sound simultaneously. What you say in substance is that simultaneity is a relative idea, for what may be perceived as simultaneous by one observer may appear to another observer as separated by a time-interval.
That succession, too, is a relative notion may be exhibited as follows: Consider two cannons, A and B, situated 5000 feet apart, and two observers, X and Y, situated on the line AB, the distances being respectively XA = 5000 and BY = 5000. At 12:00 noon cannon A fires a shot, at 12:03 this is followed by a shot from B. The shot from A reaches X at 12:05 and Y at 12:10; the shot from B reaches Y at 12:08 and X at 12:13, assuming that sound travels at 1000 feet per second and that the atmospheric conditions are normal. Thus, according to X, the shot from A preceded the shot from B by 8 seconds, whereas, according to Y, A followed B within an interval of 2 seconds.
In both these examples the relative character of temporal succession, and even of the time-interval which separates two events, is readily recognized. When, however, two positions of the same moving body are involved, our attitude changes completely. Consider, for example, the following situation. An invalid in a wheel chair has been moved from one end of the deck of a moving steamer to the other. What is the distance covered? You at once recognize that the question admits of no absolute answer: with respect to the steamer the distance is the length of the deck; an observer on the shore would have to add or subtract, as the case might be, the distance covered by the steamer; relative to the sun, the calculation would have to take into account the several thousands of miles which the earth has covered in the interim; with respect to the fixed stars, the tremendous distance traversed by the solar system in its flight [Pg 74]towards the constellation of Hercules. In short, the distance between any two positions of a moving body is not the same for all observers: it depends essentially on the reference system.
If, on the other hand, you were asked whether the same relativity obtained for the time consumed in moving the chair, you would without hesitation reply in the negative. You would say that the time-interval was the same for the invalid, for the individual who pushed him, for an observer on the sun, the moon or on any other star, provided, of course, that the clocks used by these observers had been synchronized to begin with, and then kept in perfect synchrony throughout the transition. If further asked as to how you would go about establishing such universal synchrony [S], and how, once established, you would maintain it, you would probably reply that this was a mere matter of technical detail which did not affect the crux of the problem; that the possibility of such synchrony was guaranteed by the very conceptions of space and time on which physics rests.
In all these contentions you would be fully justified from the standpoint of classical physics, which identifies the universe with a three-dimensional manifold all points of which are provided with synchronous clocks, all clocks pointing to the same time, cosmic time; the time-interval consumed in the movement of a body was just the arithmetic difference between two records of cosmic time, and inasmuch as either record was independent of the idiosyncrasies of the observer or of the peculiarities of his post, the same held for their difference.
At this juncture I shall introduce a term which was rarely heard in the classical days, but which since the advent of the relativity theory has been raised to the rank of a fundamental concept of physics. The term is signal [S]. Any phenomenon which may serve to convey to an observer an event which has occurred at some distance from the observer's post is a signal. Any one of the physiological senses of the observer may act as the "receiving end" of the signal: thus, the sense of smell may convey to a traveler the proximity of a linoleum factory; the elastic vibrations transmitted to the foot by a steel rail may [Pg 75]warn an individual of an approaching train long before the latter is heard or seen; the sound of a detonation may acquaint one with a distant explosion; the sight of smoke with a distant conflagration.
What sort of mechanism could transmit such signals? This question has mystified philosophers since the earliest days of science, and has been the source of much lively physical speculation in the last three hundred years. One could, of course, call this mechanism action at a distance [A], and let it go at that; but the mind of man would not be satisfied with such a purely nominal answer. Indeed, our minds will not rest until we succeed in associating action at a distance with the propagation of one thing or another in a medium [M].
An ideal medium we conceive as homogeneous [H] and isotropic [I], which, perhaps, is but another way of saying that an ideal medium would permit the special signals for whose benefit it has been designed to propagate in a uniform [U] and rectilinear [R] fashion. If observation reveals deviations from the straight and steady course, one usually seeks and, eventually finds, some disturbing factor or factors.
The notion of medium reminds one in many ways of space; yet there is an essential difference between the two concepts. Our physical intuition attributes to space perfect neutrality [N] towards all motion and action, regardless of origin or scope. A medium, on the other hand, is characterized by the circumstance that it grants a "right of way" to some motions or actions, and resists infiltration by others.
In the case of sound [S] the medium is the atmosphere. In still air, and under reasonably constant temperature, pressure, and humidity conditions, sound waves are assumed to propagate along straight lines, and at a uniform rate, which is in the neighborhood of 1000 feet per second, or about 700 miles per hour. This is a considerable speed as compared with ordinary locomotion; still it is not so great as to dwarf all terrestrial motion. To exhibit this circumstance, consider an airplane which is within a radius of 11 miles from an observation post, and is moving towards it with a speed of 350 miles an hour. [Pg 76]A sound signal emitted from the airplane would reach the post in 1 minute, while the airplane will reach it in 2 minutes.
In the case of light, matters are by far more intricate. In the first place, the speed of light is so enormous that it would take a ray but a fraction of a second to encircle the globe and return to the point of emission. Thus, insofar as terrestrial phenomena are concerned, the propagation of light may, for all intents and purposes, be viewed as instantaneous. In fact, most Greek thinkers and those who followed in their footsteps did regard the speed of light as infinite [I]. Galileo, it appears, was the first to think otherwise: he endeavored to determine the speed of light by terrestrial means, failing largely because of the paucity of the optical equipment at his disposal. However, he contributed indirectly to the eventual solution of the problem by his discovery of the Jupiter moons. Sixty-five years later, Olaus Roemer, using the periodic eclipses of these satellites as a basis, succeeded in calculating the velocity of light within a small percentage of the value commonly accepted today, which is in the neighborhood of 300,000 kilometers per second.
In the case of light, matters are further complicated by the circumstance that, unlike sound which is a purely terrestrial phenomenon, light has to operate in interstellar spaces. This imposes on the ether [E]—a medium invented for the purpose of accommodating the transmission of light, but later burdened with the additional responsibility of caring for other electromagnetic phenomena as well—requirements so weird that even the classical physicist felt occasional scruples in accepting them. It had to possess fabulous rigidity, and yet be entirely without mass; it had to be absolutely stationary, and yet capable of transmitting all sorts of vibrations; it had to be inert towards moving matter, and yet its behavior was somehow affected by contacts with matter. As time progressed, the ether became the "catch-all" of classical physics, and also its scandal eventually precipitating the present-day crisis in its foundations.
But let us return to the problem of simultaneity [S] and synchrony [S]. You sit in your home and listen to a London radio broadcast. You hear Big Ben chiming midnight, while the clock [Pg 77]of the neighborhood church is striking seven bells. Are you justified in claiming that the two events are simultaneous? Yes; it takes a wireless signal but 1/8 of a second to encircle the globe, and but a fraction of that to cover the distance between London and Washington. If you had heard the two sounds not at home, but on a fast moving airplane, your contention would still be justified, inasmuch as the speed of your conveyance would be negligible in comparison with the rate of wireless propagation. By the same token, we are justified in speaking of terrestrial time, for, by universal agreement, we could all declare Big Ben to be the official timekeeper, abolish the nuisance of longitudinal variations, and depend on radio transmission exclusively. A simple and effective procedure! Whether it will ever be adopted is quite irrelevant: what concerns us here is that there are neither logical nor operational [O] reasons for not adopting it.
These simple considerations lead us to the natural question: why not apply an analogous scheme to interplanetary and even interstellar spaces, and, by instituting a cosmic synchrony throughout the universe, render concrete that elusive universality which our consciousness attributes to duration? Such statements as that "such and such a particle was, is, or will be at such and such a place at such and such a time" would then pass out of the realm of gratuitous fancy, and acquire operational validity. The first step towards founding a universal kinematics would then be achieved, and who knows but that this would cast light on the perplexing problem of the structure of physical space which, as we saw, geometry unaided is unable to solve?
The procedure to be adopted almost suggests itself, since we have very little choice in the matter. The only signaling scheme which we can use is light [L]; in the absence of any knowledge on the structure of physical space, we may as well assume the one which is amenable to the most simple mathematical manipulations, i.e. Euclidean [G]. The same mathematical simplicity will govern our choice of the law of propagation of light through space: this propagation, we shall assume, is rectilinear [Pg 78]and uniform [U]. There remains to select our reference frame and units of length and time.
Accordingly, we pick some convenient spot on the surface of the earth, say the Eiffel Tower, for origin of space, and some convenient instant, say the beginning of a New Year, for origin of time. We determine the direction of the motion of the solar system through space, and take it for our x-axis; the plane of our planet's orbit, or rather a plane parallel to it, we take for our xy-plane, and a line perpendicular to that plane as the z-axis. Our unit of length may be the mean diameter of the earth, our unit of time the sidereal day, or some convenient portion thereof. The position of any point in space will be then defined by three numbers, x, y, z, and the distance [D] of any such point to the origin of coordinates will be given by the formula, d2 = x2 + y2 + z2.
We next select a conveniently located fixed heavenly point, H, for our first experiment. By rights we should dispatch to that point a dependable observer equipped with a chronometer and telescope; but since this is impractical, we shall do the next best thing: engage the services of a competent terrestrial observer, and appoint him as official timekeeper for the point H.
At midnight sharp on December 31 we send out from our post, T, our first signal: a flash of light. This is followed periodically by an indefinite succession of flashes separated by unit-intervals of time. Our observer by proxy, knowing the distance d = TH and the velocity of light c, calculates the ratio a = d/c, and announces that our first signal will reach H after a intervals; when this particular instant arrives, he is directed to set his chronometer on zero time.
The second signal involves slightly more complicated calculations. For, the point, T, from which the flashes are emitted, has by now changed its position in space, because of its participation in the motion of the earth as well as in the displacement of the whole solar system through space. As a result, the distance from the point of emission to the fixed point H has changed; and this, in turn, has affected the time of the ray's transit. However, our observer by proxy, after performing the [Pg 79]requisite arithmetic, informs us that our second signal will reach the point H within b intervals from the origin of time, whereupon we direct him to set his chronometer at 1, when that instant arrives.
When we attempt to repeat this performance for the third signal, our timekeeper protests. He has been hired as an observer, he says, but as matters turned out he is just a computer. In fact, he adds, he could without much trouble work out a formula and a graph which would permit us once and for always to determine the time when any one of our signals reaches the point H in terms of the time when the signal was sent out. More than that: he could construct a mechanism which would do his job automatically; this apparatus would not only correlate the local time at the point H with terrestrial time but accomplish the same thing for any other point in space, by means of an adjustment which would be as easy to handle as an ordinary adding machine.
And such is indeed the case. The net result of our hypothetical observation may be exhibited on two scales: T and H. The H-scale indicates the local time at the point H, while the T-scale gives the time recorded by the terrestrial observer at "the same cosmic instant." I shall not bore the reader with the details of construction of this diagram. It involves simple arithmetic and some rudimentary notions of analytic geometry, and the reader who is so inclined can readily derive the requisite formula and construct the two scales. I therefore pass without any further ado to the analysis of the results obtained.
This analysis is most disquieting. Not because simultaneity is not represented by identical readings: were this the only trouble, it would be trivial enough, for it could be remedied by redefining local time. And not because the interval between two successive readings on the H-scale is not equal to the corresponding interval of the terrestrial chronometer: while this circumstance is more serious, it would not be fatal to our scheme, since it could be remedied by assigning different units of time to different points. The disheartening aspect of the diagram is the [Pg 80]circumstance that the temporal series recorded at the point H is not uniform despite the fact that the signals which induced it were emitted at regular intervals.
We conclude that if from a moving source we emit at congruent intervals a series of signals which propagate through space at a uniform finite rate, then these signals will induce at any fixed point of space a series of events which, when gauged from the moving post, will not succeed each other at regular intervals. In other words, in a Euclidean space [G], with light traveling along straight lines at a constant finite rate, light signals have for general effect the distortion of temporal series.
The verdict which we have reached—for, it is nothing short of a verdict—is of the utmost importance not only to the problem of cosmic time but to the whole science of celestial mechanics. The situation which we have described in the preceding sections, far from being just another fantastic Jules Verne tale, is but a schematic presentation of the technic of astronomical observation.
Indeed, inasmuch as our argument involved relative motions only, we can think of any heavenly body as executing a more or less intricate motion about the earth, which may be conceived to be at rest. All the events on that body which fall under our observation are then so many light signals; the assumptions which we have made on the "texture" of physical space and on the propagation of light are identical with those of classical astronomy; the only difference between the actuality of classical astronomy and the fiction of our illustration is that the roles of the observers T and H are now interchanged. It follows that the verdict which we have reached in one case holds for the other.
This means that the classical conception that events outside our planet follow time schedules which are independent of the terrestrial astronomer who observes them is untenable from the operational point of view. In other words, light signals have signally failed us in materializing that universal synchrony [S] which our mind attributes to duration. Why has the scheme failed us, and is the failure irremediable? Was the failure due to our specific [Pg 81]assumptions, or to the inherent impossibility of correlating physical time with duration?
Perhaps, by positing a space structure other than Euclidean [G], we could eliminate the difficulty that in the process of signaling time-congruence is destroyed. No: it can be readily shown that, regardless of the structure assumed, so long as we insist on a finite velocity [V] of propagation, time-congruence will not be preserved. If, on the other hand, we decided to return to the pre-Galilean period, and declare the speed of light infinite, then regardless of the space structure assumed time-congruence and simultaneity would be preserved. This, of course, is but another way of saying that if we could identify the speed of light with the speed of thought, then physical time would possess the same attribute of universality as psychological time, for which duration is but another name.
I admit that one could measure accelerations by waiving the difficulties incident to measuring time. But how can one measure force [F] or mass [M], when we do not even know what they are? . . . When are two forces equal? Will you answer that two forces are equal if they produce the same acceleration [A], when applied to the same mass? Or, if they balance each other when they are directly opposite? But this definition is but a sham! One cannot detach a force applied to a body and attach it to another body like one uncouples a locomotive to couple it onto another train.
Henri Poincaré, On Classical Mechanics
WE ARE confronted in regard to both space and time with an indeterminacy repugnant to the mind [E]. To the latter, space is an immobile, rigid, all-pervading web; time a continuous, uniform stream which carries the universe in its flow. And yet thus far we have been unable to uncover a single phenomenon which would reassure us that these attributes of space and time are anything more than anthropomorphic hallucinations.
Shall we then give up the quest as hopeless? No. For thus far we have confined our efforts to purely geometrical and kinematic considerations. Geometry, after all, studies a stationary universe; it is an abstract fictitious world it studies, a world in which time is conceived as having momentarily arrested its otherwise inexorable flight. Kinematics [K], too, deals with a fictitious universe, for, while it gives lip-service to time, it is not the mysterious stream of consciousness it deals with. Time to the kinematician is just a parameter, a mere term in which he can [Pg 83]conveniently express changeable distances, angles, or the like. It was not on such abstractions that our intuition was reared.
There are many other manifestations of the physical universe which the geometer and the kinematician purposely ignore: gravitation [G], the electromagnetic phenomena, heat. There are many other physical concepts: mass [M], force, energy, temperature [T]. To these we shall now repair, in the hope that they may lead us out of the labyrinth of perplexities into which the study of space and time has driven us.
If intellectual achievements were hailed with the fervor reserved today to military deeds, then 1938 would have been the year of a great international festival at Florence, commemorating the tricentenary of the birth of modern science. For, in the year 1638 appeared Galileo's [G] last work Dialogues on Two New Sciences. The author was then 72, blind, ruptured and afflicted with an assortment of other ailments. He had been living in detention in a villa in Florence under strict surveillance of the agents of the Inquisition. In the five years which elapsed since his condemnation he had become an almost legendary figure. The ingrained stupidity of the Inquisition had only served to exaggerate his martyrdom in the eyes of the world. Thus, even a book of inferior quality would have been eagerly taken up by a sympathetic public. But far from being a product of a senile and broken spirit, the Dialogues on Two New Sciences was Galileo's greatest achievement: for wealth of ideas, beauty of style and clarity of thought, this swan song of the master has no equal in scientific literature.
Here were laid the foundations of the modern science of mechanics. The principle of inertia, the conception of force as the genesis of non-uniform motion, the ideas of action and reaction, of composition of movements, of relative and absolute motion, and many other concepts so familiar today that they almost appear to us as commonplaces—found their first expression in these Dialogues. On these ideas Newton [N] fifty years later erected his famous Principia. It is no exaggeration to say that without the principles formulated in the Dialogues and the Kepler [K] Laws, Newton could never have conceived universal gravitation which, [Pg 84]by offering the first rational interpretation of planetary motion, made the Copernican [C] theory incontrovertible in the eyes of succeeding generations.
One of the epoch-making ideas contained in the Dialogues was a postulate which has played as great a part in the history of dynamics as did the Euclidean postulate in the history of geometry. This postulate, reformulated in more explicit terms by Descartes [D] and accepted by Newton as the cornerstone of his mechanics, is known as the principle of inertia [I]. It consists in the assertion that: An isolated [I] particle of matter, i.e., a particle free from all external influences, will either remain at absolute rest, or else move with absolute uniformity along an absolute straight line.
The principle is susceptible of several paraphrases. Thus, it may be formulated in terms of conservation: Nature, it may be said, is bent on preserving some physical attributes, such as the forms of rigid bodies, the quantity of matter in any body, or the energy contained in a system. Straightness [S] and uniformity of motion are also among the attributes which Nature endeavors to conserve. In the words of Descartes: "Any portion of matter will remain forever in the same state, unless encounters with other matter constrain it to a change; thus, if it possesses magnitude, it will never become smaller, unless other material bodies divide it; if it be round or square, it will never change this form, unless other bodies constrain it thereto; if it be arrested in some place, it will never leave the spot unless others drive it away; and if it had once begun to move, it will keep moving forever and with constant speed, unless other bodies stop or retard it."
One could also interpret the principle of inertia as disguised attributes of space and time. For, it implies that space is so constituted as to put no obstacles to the motion of a body which would follow the "straight and steady" path, but resists any attempt to depart from such a course. In a similar manner, time offers no opposition to uniform [U] motion, inasmuch as uniformity is one of its own attributes, but penalizes all deviations from "constancy".
[Pg 85]This non-resistance of Nature to the straight and the steady constituted a radical departure from the views of the ancients. To the latter, rest alone was perfect; nature abhorred all motion: straight, curvilinear, uniform, and irregular alike. Nature resisted all movement; to overcome this resistance it was necessary to exert a force; the greater was the speed one desired to maintain, the greater force one had to supply; resistance to motion was regarded as proportional to velocity.
Such assertions are partly supported by the evidence of the senses. Thus it certainly takes a greater effort to walk fast than slow; the strain experienced while stopping a moving body certainly increases with the body's speed. In all probability, it is to such physiological considerations that the concept of force owes its origin; eventually, through a sort of "animism" which marks most early speculation, these notions were transferred by man to nature.
Aristotle's contention that, all things being equal, a heavier body would reach the ground sooner than a lighter dropped from the same height was based on some such argument as this: Since force varies with velocity, so, conversely, there must be greater velocity wherever a greater force is observed; thus when a ten-pound and a one-pound weight are dropped simultaneously from the same height, the forces which pull them to the earth are in the ratio of one to ten; the corresponding velocities must be in the same ratio; in other words, the velocity of the heavier is ten times greater, and since both cover the same distance, it will take the lighter ten times longer to reach the ground.
One can understand the consternation of the spectators who watched Galileo's [G] experiment at Pisa, and appreciate the boldness of the Galilean conception which seemed so contrary to common sense.
Can the principle of inertia resolve at least some of the perplexities raised by the problems of space and time? Can it, in particular, offer satisfactory answers to the elusive queries: "What is straightness? What is uniformity?"
At first sight it would appear that such is the case. For does not the principle take for its point of departure the uniform [Pg 86]and the straight? Does it not inform us that straight is the path of a freely moving particle, and that uniform is the rate at which it moves? Does it not suggest a design for that perfect clock which we have in vain sought to attach to some periodic motion? It should, indeed, be sufficient to choose once and for always the motion of some completely isolated particle for standard, and adopt for unit of absolute time the interval consumed by this particle in traversing a unit length. The principle of inertia would then guarantee that, in the absence of any cause that may accelerate or deviate the particle, equal lengths will be covered in equal times. While the principle does not define either congruent lengths or congruent time-intervals, it does apparently formulate a relation between time-congruence and space-congruence, a relation which could, perhaps, be utilized to reduce one to the other.
Whatever the founders of classical mechanics would have thought of the validity of such ideas, from the standpoint of modern physics these arguments are entirely inadequate: they merely shift the difficulties inherent in our intuitive notion of space and time to a concept even more intricate and vague. What does one mean by absolute isolation? How can one judge whether any given particle of matter is free, unless it be by the circumstance that, when set in motion, it will describe uniformly a straight line? It is a vicious circle this formulation of force by the absence of uniformity, and of uniformity by the absence of force.
Absolute isolation is a myth: there are no isolated systems, nor can we artificially produce isolated experiments. There is not a single material particle in our environment regarding which it may be rigorously maintained that it is entirely exempt from the influence of all other bodies in the universe. What the principle of inertia tells us may be summed up in the words: if we had complete isolation, we would have uniform motion of particles, provided we had particles. If we had ham, we could have ham and eggs, if we had the eggs. There is but one step from the sublime to the ridiculous.
But if absolute isolation is a myth, what of the principle [Pg 87]which depends on the possibility of such absolute isolation for its very life? And if the principle is void of physical significance, how should one account for the circumstance that for more than two centuries it acted as cornerstone of a mechanics which had rendered so many signal services to science and technology?
The situation resembles strongly the one we encountered while analyzing the concept of absolute space. I remarked at the time that Newton's [N] definition of absolute space was like a pious invocation with which the labor of a day began, but which had no other bearing on the day's labor. For, by accepting Euclidean geometry, Newton also accepted the relativity [R] clause which that geometry implicitly contained: namely, that the laws governing geometrical form and magnitude would be the same for a moving observer as for an observer at absolute rest.
The absolute isolation implied in the principle of inertia was just another such declaration, piously invoked, but never used. The pragmatic successes of mechanics were achieved not through the principle of inertia, but by applying the so-called fundamental equations of dynamics, and these equations rested on a far more significant principle of which that of inertia was just a hypothetical limiting case. It will be expedient to designate this more general conception as the extended principle of inertia.
When we survey the dynamical activity in our environment, we observe many motions which are neither rectilinear nor uniform. What is more, far from being exceptional, these "irregular" phenomena predominate. In fact, the straight and uniform motions are not only rare, but, as a rule, rather unstable, so that the maintenance of any such steady state [S] for any length of time requires artificial measures. If then we accept the restricted principle of inertia as the basis of our dynamical speculations, we must assume the existence in nature of a vast aggregate of disturbing causes which deviate moving bodies from their "regular" paths. Let us agree to call any such disturbance a force. Obviously, such a definition is a mere paraphrase of the restricted principle of inertia, and does not even begin to touch the problem, which is to so formulate the concept of force as to make [Pg 88]it amenable to measurement and calculation, preserving at the same time its qualitative attributes. The extended principle of inertia offers a simple solution to this dilemma.
Consider the case when the motion is rectilinear but not uniform. Here the disturbance, whatever it might be, manifests itself in the rate of change in the rate of speed, a quantity which is called acceleration [A]. Like speed itself, this entity may be measured by means of a graduated stick and a chronometer. In other words, acceleration is a magnitude, a number, which may be positive, negative, or zero.
Thus, in the case of rectilinear motion, the effect of the disturbing cause is purely kinematical; and since it is natural to measure any cause by its effect, the most simple solution of our problem is to assume the force [F] to be proportional to the observed acceleration. There remains the question as to whether such a dynamical [D] definition of force agrees with certain static [S] ideas on force developed in the course of many millennia of experience in overcoming obstacles to action. To bring out the importance of this question, I shall consider some familiar motions.
A stone is dropped from a height; gravity pulls it downward with the result that it describes a vertical straight line acquiring greater and greater speed as it falls. Then it reaches the ground, and there it suddenly comes to rest. What has happened? Has gravity ceased to exist? No! We have but to pick the stone up to realize, by the effort exercised, that gravity still acts; for instinctively we identify the static effect of the force which is measured by this effort with the dynamical aspect of gravity which "caused" the body to fall.
But, if the force still exists, why does it not produce acceleration as all well-behaved forces should? Why does the stone remain at rest? How indeed can anything remain at rest in the presence of forces? It is a perfectly legitimate question, for, it is just pushing the principle of inertia to its logical limit. What is the answer? Could it be that it is as difficult for the principle of inertia to account for the existence of rest as it was for the Greek thinkers to account for the existence of motion?
[Pg 89]Galileo [G] overcame this difficulty by postulating the existence of inactive forces which Newton later called reactions [R]. If a body remains at rest, it is that some reaction has counterbalanced the active forces in the field; the resultant of all forces, active and reactive, is zero; thus all disturbing influences neutralize each other, the particle acts as though it were isolated, no motion occurs, and the principle of inertia is saved.
These reactions solved an even more general problem: it is as difficult indeed to account for the existence of "regular" motions in a field of force, say, in the gravitational field of the earth, as it is to explain rest, for, the principle of inertia makes no distinction between rest and uniform translation [T]. How, for instance, can a bird fly in a straight line, and with constant speed at that, in the teeth of gravity? The answer is that the resistance of the air is at any instant balancing the gravitational pull, producing a zero resultant. How can a ball roll down an inclined plane in a straight path, and uniformly at that? The friction of the surface accounts for this. Why do the particles of a solid body stay put, instead of flying asunder under the action of gravity? Cohesive internal forces keep them together. Whenever and wherever a violation of the principle of inertia is observed, it is sufficient to invoke some reaction to have the difficulty vanish, as though by magic.
Let us examine the situation at closer range. You hold an object in your hand; it is at rest. "Still," you argue, "some force must be acting here, for how otherwise could I account for the strain in the muscles of my arm?" You release the object; it begins to move with increasing speed. What could be the cause of this accelerated movement? You argue that the same force of gravity which was responsible for the muscular strain in your arm while the body was at rest, produces the accelerated fall of the released body. This is a qualitative statement. "However," you argue, "I can substitute for my muscle a static balance which will measure my physiological effort in kilograms; I can determine the acceleration by means of a measuring rod and a chronometer and thus express it in centimeters per second; I shall obtain in this manner two numbers, F1 and A1, of which [Pg 90]the first represents the force and the second the acceleration."
You next fasten the same object to the end of a stretched rubber band and hold it there. Again your muscles inform you of the existence of a force; again the static balance gives you the magnitude, F2, of that force. You now release your hold, and the object begins to move: you measure as before the acceleration at the instant of release and obtain a number, A2. You perform analogous experiments in most variegated fields of dynamical activity—magnetic, electrical, centrifugal—but always with the same body, obtaining on the one hand a set of numbers F, and on the other a set of numbers A. You correlate these results, and find that if you divided each F by the corresponding A, you would be led to the same number m, or in symbols:
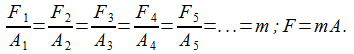
You conclude that the ratio of the force to the acceleration is a constant; that this constant is independent of the field of force, or of the magnitude of the force, or of the motion in which the object is engaged; that it is something inherent in the object itself. This constant m may be called the coefficient of inertia of the object. The extended principle of inertia takes on the very simple, yet fundamental form: F = mA. This formula, apparently, is not an identity, not a definition, not a mere tautology: it has all the earmarks of an experimental fact, of a law of nature [L].
This is a remarkable proposition, but even more remarkable is the precision with which this law fits all observation. For—unlike other experimental laws where mathematical simplicity is achieved at the expense of secondary effects and must, in turn, be sacrificed when greater precision is required—we find in the case of the extended principle of inertia that the greater the experimental safeguards exercised in checking its validity, the better the law seems to agree with the evidence.
The agreement is perfect, too perfect indeed to be comfortable. Our excursions into the intricacies of space and time [Pg 91]have amply demonstrated to us that certain concepts, elementary as they may appear to a mind which is not in the habit of reflecting on such issues, derive their force from other notions, just as imperative and, in the last analysis, just as elusive. In vain did we try to reduce to experience such ideas as rigidity [R], straightness, uniformity [U], simultaneity: like the notions of the infinite, of the rational character of the universe, or of the causal concatenation of events, these ideas seem to antedate all experience. They do not describe experience; at best, they insinuate the structure of the collective mind which organizes, records, and stores the accumulated experience of the race.
Is the principle of inertia just another of these collective predilections, so subtle this time that it escaped the vigilance of even the most critical physicists of the eighteenth and nineteenth centuries? Was the classical scientist so busy piling up corollaries to this law that he let the law itself escape the acid test, like that proverbial bride who in her preoccupation with the trousseau forgot to keep a weather eye on the elusive groom?
Or have we at last struck a truly objective [R] law, a true reflection of an aspect of the external world, the source of all experience? If the principle does possess such objective validity, then perhaps it will help us to clarify some, at least, of the perplexing issues which we have encountered in this study. For, implied in the very statement of the extended principle of inertia are most of the fundamental concepts of the science of physics: time and space; matter [M] and force; cause [C] and effect.
Matter to us is something tangible, palpable, concrete; perhaps, the one truly concrete aspect of our experience. Still, like so many other physical ideas, this concept must submit to a drastic Procrustean operation to be rendered mathematically articulate. When it emerges from this operation, it is far from being the tangible, palpable thing we started with; however, what it has lost in concreteness it has gained in generality. While the new concept is not as amenable to sight and touch as the crude idea from which it arose, it is amenable to number. Most physical concepts passed through a similar evolution, but the story of matter is especially eloquent in this regard.
[Pg 92]The crux of the matter is that although matter is among our most direct perceptions, we lack the means of measuring it directly. We compare the quantities of matter contained in two objects either by the volumes they occupy, or by the relative resistance which they offer to some attempted action, such as lifting, rolling, or dragging. Of these two methods, volume [V] is in better agreement with our physical intuition; however, it may be applied only in the case when the two objects are made of the same "stuff," whatever this may mean; furthermore, even in this case the method is rather unreliable, and certainly inconvenient, if not impractical. This leaves little choice: thus, ages before the principle of inertia was formulated or even thought of, man expressed mass [M] in terms of weight, identifying for purposes of measurement matter with force. But for purposes of measurement only. The momentary hesitancy with which the average individual responds to the "booby" question as to what weighs more, a ton of hay or a ton of lead, is ample evidence of our inherent reluctance to associate matter with resistance.
Matter to our mind is that something possessed by every movable object, which cannot be destroyed or even changed, however intricate or however violent be the motion to which the body is subjected. We cannot identify this permanence with form, because of the existence in our environment of bodies other than rigid. We cannot identify this permanence with volume, i.e., with the space occupied by the movable object, because this magnitude is itself a variable in the case of gases. How, then, could we render this important concept of mass mathematically articulate?
The principle of inertia suggests a very convenient answer to this query. Explicit in its formulation is a magnitude which we called coefficient of inertia; like the intuitive idea of mass, this coefficient is independent of the motion to which the body may be subjected. Why not identify mass with this coefficient of inertia?
. . . There is no need for a definition of force: the idea of force is primitive, irreducible, undefinable. We know what it is, because we possess a direct intuition of it, an intuition derived from our notion of effort familiar to us since infancy. But even if this direct intuition gave us an insight into the true nature of force, it would not only be insufficient to found a mechanics, but altogether useless. For, what matters is not knowing what a force is, but knowing how to measure it . . . Besides, the notion of effort does not convey to us the true nature of force. It is just a recollection of a muscular sensation, and nobody would support the idea that the Sun experiences a muscular sensation when it attracts [G] the Earth.
Henri Poincaré, On Classical Mechanics
OUR intuitive idea of cause is hardly more than a confused feeling that certain events do and, therefore, must follow one another in a definite temporal order. Here too the principle of inertia substitutes for a hazy notion a formal concept, susceptible of measurement and calculation.
The intimate kinship between inertia and causality is already apparent in the restricted principle. Indeed, the latter asserts that no acceleration is possible without a force [F] being present. Interpret acceleration as effect, force as cause, and you have here a sort of "negative" formulation of causality [C]: there cannot be effect without cause. The extended principle of inertia goes even further: it undertakes, in matters mechanical at any rate, to reduce causation to measurement, by formally identifying cause with force.
This fertile idea, first formulated by Newton, paved the way to that eventual mechanization of physics which the nineteenth century saw so nearly consummated. It led to the conception of mechanical work, and from that to energy [E], thus linking motion [Pg 94]to the vast aggregate of other phenomena which were ceaselessly changing matter. This, in turn, led to regarding any physical transformation as motion in disguise, or, which amounted to the same thing, to regarding motion as the basic phenomenon to which any other might be potentially reduced. By the same token, all causes would eventually become reducible to forces; i.e., to mass and acceleration. It was an ambitious program, and yet early in our own century the goal was clearly in sight.
We saw, on the other hand, that the extended principle of inertia identifies two ideas which, however plausible their mathematical equivalence, differ essentially in origin. One is the dynamic [D] force presumably responsible for the deviations of a moving body from the straight and steady course, the other the static [S] force which manifests itself in the resistance of a stationary body to motion. It would have been contrary to the ideology of the classical physicist to accept such an identity as a mere convention. He sought an explanation, i.e., an analogy with a more familiar situation.
The behavior of fluid media seemed to offer such an analogy: for the reactions set up in a fluid by a body in motion have all the earmarks of genuine field forces, and resemble at the same time static resistances, such as friction, for instance. Thus if it were possible to view empty space as a ponderable medium, an ether, and view the forces which perturb dynamical equilibrium as so many resistances, then a plausible explanation of this remarkable equivalence between force-cause and force-resistance would be potentially at hand.
But this is not all. Such a model-medium would offer a "solution" to still another riddle which had been perplexing speculative physicists since the days of Descartes: the mysterious action at a distance. We saw in the last chapter that the sundry attempts to design such an ether had failed because of the many conflicting requirements which the medium [M] had to satisfy. These failures eventually led the physicists to give up the notion of ether, at least in the classical sense of the term. However, the interpretation of forces as stresses [S] in a medium was altogether too seductive an idea to be permanently abandoned: in the new guise [Pg 95]of spatial curvatures [C] it has found a modern reincarnation in the pattern of the general relativity [R] theory.
We know that the propounder of universal gravitation [G] was himself much perplexed by the riddle of action at a distance, and that at one time he too had toyed with the idea of an ether. The pressures created in this hypothetical medium by material bodies immersed therein were to account for the mutual attractions of these bodies, attractions which, according to his law of gravitation, were responsible for the relative motions of these bodies. Newton [N] never published his reflections on this subject, "because," using his own words, "experiment and observation would not give a satisfactory account of this medium, and of the manner of its operation in producing the chief phenomena of nature." Invoking his famous slogan hypotheses non fingo, he resolved to be content with the purely mathematical formulation of universal gravitation.
For purposes of calculation the law of universal gravitation, reinforced by the principles of inertia, action and reaction, and composition of motions, was quite sufficient. Indeed, upon perusing Newton's Principia, one cannot escape the feeling that these principles were sort of afterthoughts designed to lend to the law of gravitation the requisite mathematical decorum. And it may be stated that while the calculating apparatus of classical dynamics did rest on these principles, without a law of gravitation there would be hardly anything to calculate. Indeed, the greatest triumphs of classical dynamics were achieved in fields where gravitation, in one guise or another, had been taken for granted; and it is safe to say that without a law of gravitation the equations of dynamics would be just mathematical exercises, and the principle of inertia with all its ramifications would lose physical significance, inasmuch as it would not be susceptible of experimental verification.
I said without a law, using the indefinite article advisedly. The assumption that the force of attraction between two particles was inversely proportional to the square of the distance between the particles was introduced by Newton because no other simple [Pg 96]mathematical law would have satisfactorily accounted for the elliptic orbits of the planets. In principle, however, it mattered little whether the attraction was inversely proportional to the square, the cube, or obeyed a much more involved law; what did matter was that the force of attraction was independent of the velocities of the bodies, that it diminished with the distance between the two bodies, and that it would tend towards zero, if the distance grew beyond all pre-assigned limits.
What mattered even more was a conception, explicit enough in the writings of Descartes but which had never been stated in so many words either by Newton or by his followers, although it dominated all their physical speculations. It was the conception that without matter [M] there would be no force; that any force might be traced to some action of matter; that matter was the cause of all perturbations in the dynamical equilibrium of any system, whether it be the universe at large, or the smallest part thereof.
Conceive all matter momentarily removed from the universe [I]: according to the classical physicist, this act will not affect the flow of time nor alter the structure of space. Release into this empty space a material particle: in virtue of the principle of inertia, this lonely lump of matter will either remain at eternal rest or, if given an initial impetus, proceed along a straight line, covering equal distances in equal intervals of time.
Release a second particle. This act creates a force which deviates the first particle from its straight and steady course. The acceleration which measures this deviation is, according to the principle of inertia, proportional to the perturbing force; the force, however, in virtue of the law of gravitation, depends only on the masses of the particles and on their distance apart. Thus the course of the first particle may be predicted for all time to come, and the same is true of the second particle. This mathematical exercise is known as the problem of two bodies [T].
Release a third particle. The problem becomes more involved: two forces now act on each particle; in virtue of the principle of composition of forces, however, the two forces may be viewed as one. It is true that the resultant follows a more complicated law than do the components; still, this resultant, too, [Pg 97]depends only on the masses of the particles and on their relative positions. Consequently, the problem of three bodies [T] may also be turned into a mathematical exercise, and the courses of the particles forecast for all time to come by solving a system of differential equations. The same is true of any number of bodies. To be sure, with each additional particle the calculations become more involved, whilst the requisite mathematical apparatus may grow so complex as to challenge the ingenuity of a Poincaré; however, these difficulties are mathematical in nature, not conceptual.
You say that only a god could enact such wholesale destruction and re-creation of matter? Well, he who would cultivate mathematics should not hesitate to put himself on occasion into the shoes of a god. You say that the physicist is denied such divine prerogatives, that he not only calculates, but measures? I grant that this is quite a handicap; still, things are not as bad as they may first appear. Absolute physical isolation [I] is a gratuitous assumption, but quasi-isolation is not, at least not to one who accepts the universal law of gravitation. For in a region sufficiently remote from other matter, a moving particle is subject to forces so feeble that they may be readily ignored. Accordingly, such a quasi-isolated body would describe a quasi-straight line at a quasi-uniform rate. Similarly, the mathematical solution of the problem of n bodies may serve as a satisfactory approximation to the physical situation created by n bodies moving in a vast region free from other matter. To estimate the "goodness" of such an approximation may be a subject of great difficulty, but such difficulties, too, are mathematical, not conceptual.
Conceptually, the whole matter was settled from the very outset. The assumptions that space was everywhere flat; that universal time was a physical reality; that associated with any particle of matter was a constant numerical coefficient, its mass, which was independent of the position of the particle, or of the field of force which acted upon it, or of the motion into which the particle might engage; that the law governing the interaction between material particles was the same everywhere; that, consequently, the mathematical function which expressed the relation [Pg 98]between force, distance, and masses could be determined by terrestrial experiments and astronomical observations within the solar system, and then extrapolated for the universe at large, or interpolated for micro-phenomena—these assumptions determined the universe of discourse of classical physics so exhaustively that Newton could well afford to close the door on all further speculation by a firm hypotheses non fingo.
These assumptions abounded in incongruities; yet these incongruities were not of a type which could be detected by direct argumentation or direct experimentation. They lay hidden behind a set of metaphysical tenets, tenets so plausible as to appear incontrovertible. The essential unity of nature and the rationality of its laws was one of these tenets: this led the scientific quest for a unique pattern which would fit all phenomena of nature. That what was valid in the observable world was valid for the universe at large, was another such tenet: this turned the study of matters inaccessible to direct observation into problems of interpolation and extrapolation [E]. That it was possible, potentially at least, to render any observation independent of the idiosyncrasies of the observer and of the peculiarities of his post, was a third such tenet: this relegated the conceptual difficulties inherent in a physical problem to questions of experimental refinement or mathematical skill.
The incongruities incident to the classical conceptions of space and time were the subjects of the preceding chapters. There remains to show that analogous incongruities resided in the classical concepts of mass and force, and this leads us to an analysis of the principle of relativity.
The classical principle of relativity, like the principle of inertia with which it is closely allied, is susceptible of a number of formulations. One of these consists in the statement that an observer whose post was moving in uniform translation [T] would reach the same conclusions in matters mechanical as another observer whose post was at absolute rest. Either observer could maintain that he was standing still while the other was moving, but both would have to admit that, insofar as their mechanical [Pg 99]experience was concerned, the alternative opinion was just as tenable.
Slightly paraphrased, the principle states that the laws of mechanics as derived by an observer whose post was moving in uniform translation would be identical with those derived by an observer at rest, provided both observers confined their observations to purely mechanical events. Thus formulated, the scope of the principle of relativity is as broad as that of mechanics. If we say that mechanics deals with position, velocity, acceleration, mass and force, then any relation involving these entities is a law of mechanics, and any phenomenon which may be expressed in terms of these entities is a mechanical event.
Now, we saw that the evolution of classical physics had been in the direction of subordinating all branches of physics to mechanics. First sound, then heat, then electricity, magnetism, and light, and finally molecular and atomic phenomena, received mechanical explanations, until at the close of the last century the line of demarcation between mechanics and the rest of physics grew so faint as to be almost indistinguishable. With each successive step of this mechanistic conquest, the principle of relativity grew in scope, until the original restriction became almost meaningless. The principle could be rewritten to read: the laws of nature as they appear to an observer whose post is moving in uniform translation are identical with those which would be derived by an observer whose post was at absolute rest.
Then, at the turn of the century, the serenity of the scientific outlook was rudely disturbed. The celebrated experiments of Michelson [M] and Morley [M] revealed that an immobile ether [E]—the elastic space-filling fluid which had been designed for the express purpose of subordinating optical and electro-magnetic phenomena to the laws of mechanics—was incompatible with the classical principle of relativity. The physicist was faced with the choice of either partitioning physics, or revising the foundations on which it rested. The second alternative prevailed. The revision took the form of the Special Theory of Relativity of Einstein [E].
What concerns us here is not the bizarre consequences [Pg 100]which the new theory entailed, or that an old and honored principle had to be drastically changed to fit new facts. The revolutionary aspect of the new doctrine was its invasion of the sacred precincts of space and time. Moreover, once the floodgates of restraint had given way, there was no turning back. A searching critique of the remaining concepts of physics soon followed, a critique which eventually culminated in the General Theory of Relativity.
In the year 1916, when Einstein [E] announced his General Theory, there died unheralded a physicist who today is recognized as Einstein's precursor in this order of ideas. The name of this physicist was Ernst Mach [M]; before his retirement he had occupied a chair of philosophy at the University of Vienna; yet he was no more a philosopher in the traditional sense of that term than Poincaré. "The land of the transcendental," he wrote, "is closed to me. What is more, I openly admit that the inhabitants of that land arouse in me no curiosity whatever. I add this in order that the chasm which separates me from philosophers may be duly appreciated."
The contribution of Mach which is of particular importance to this study is his critique of the Newtonian [N] ideas on absolute motion. We saw that according to the classical principle of relativity an observer following uniformly a straight line would have no means at his disposal to detect the motion. For, only through the play of forces could any observer recognize a motion in which he was participating, and the very fact that the observer moved in uniform translation proved that there were no forces at play. This was but a corollary to the principles of inertia [I]. On the other hand, if the observer's post moved in an accelerated [A] manner, he could not help but know that he was moving. For just as a field of force acting on a free body produced accelerated motion, so, conversely, a system constrained to follow an accelerated course would induce a field of force. This field of force was bound to react on the observer and render him aware of the accelerated motion of his post.
Such was the contention of Newton. To illustrate: Consider [Pg 101]two laboratories, A and B, identical in equipment and manned by observers with identical trainings and outlooks. Assume that A is moving uniformly along a straight path, while B is being propelled around a circular track. The observer in A could maintain that he was at rest, for there would be nothing in his experience to contradict such a statement. But the observer in B would be compelled to declare that he was moving, for, he could not otherwise account for the centrifugal forces [C] induced by the circular motion of his post.
Such arguments Mach [M] would regard as specious, to say the least. He would hold that the observer B had as good a right as observer A to declare that his own post was immobile, even if he were fully aware of the centrifugal forces at play. For there was nothing to prevent him from interpreting these inertial forces as action of some gravitational field. The circumstance that it would have been rather difficult for the observer to trace the source of such gravitation [G] has nothing to do with the argument. The only thing that really matters here is that, insofar as the observer's experience is concerned, the static explanation is as tenable as the dynamic one.
Mach's contemporaries regarded his ideas on absolute motion as so many impractical proposals of an over-critical mind. And it must be admitted that to a certain extent they were right. For his was a program rather than a theory. The practical execution of the program, had he attempted it, would have been fraught with insuperable obstacles. The solution which the modern theory of relativity offered to Mach's problem required not only the combined resources of modern analysis and geometry, but a veritable revolution in the classical views on space and time, a revolution which Mach could not have foreseen.
Yet, his labors had not been in vain. For, out of the seed which he had planted there blossomed forth later a doctrine which in boldness and scope surpasses anything that had hitherto been attempted in the realm of science. The basis of this doctrine is the principle which declares that however involved may be the relative movement of an observer and his observata, the observer [Pg 102]has always the choice between two alternatives which are equally justified from the standpoint of logic and experience: he may view his post as immobile, and attribute the play of forces which his senses or his instruments record to the action of a gravitational field; or he may regard his observata at rest and his post in motion, and interpret his experiences as the action of inertial forces induced by the accelerated motion of his post.
To present this principle in sharper relief, I shall resort to one of those thought-experiments of which I have made frequent use in this book. The world which I shall ask the reader to conceive is not unlike the spherical pseudo-universe of Poincaré which I discussed in an earlier chapter. This particular sphere, however, is revolving at a high speed about a fixed axis which passes through the center of the sphere; moreover, it is bounded by a glass enclosure which confines the species that inhabits it to the interior, but, at the same time, renders them aware of the existence of a world outside their own.
Now, if this species be endowed with a consciousness and an intelligence akin to ours, they will be led to regard their world as immobile; by the same token, they will declare that the world beyond their enclosure is executing a periodic revolution about a diameter of their sphere. Any material particle in the interior of their sphere will be actuated by a force proportional to the mass of the particle and its distance to the axis; these forces will tend to propel all objects away from the axis, with the result that the species will be constantly called upon to exert efforts to maintain themselves and their belongings in equilibrium. We would account for this behavior of things by the centrifugal forces induced by the rapid spinning of their world. Their physicists, however, will maintain that this behavior is due to the existence of a gravitational field which varies directly as the distance to the axis. Furthermore, extrapolating their experience beyond the enclosure, they will conclude that the periodic motion of their external world is also brought about by that gravitational field.
In vain would we attempt to convince these beings of the errors of their ways of thinking, for we could not suggest a single [Pg 103]experiment which would bring out that their world was revolving, while the external world was at rest. We would, at last, resolve to resort to extreme measures and say: "We hate to do it, but since you would not be persuaded otherwise, we shall arrest the motion of your sphere: your so-called gravitation will then disappear as though by magic, and you will thus realize that it was no gravitation at all, but merely inertial forces induced by the motion of your world." Would this Draconian plan convince our adversaries? It would not. If they should at all survive the catastrophe, they would counter: "Our forces have disappeared. But we are not deceived! You did not arrest the motion of our world, because there was nothing to arrest. What you did do was to annul the gravitational field, by removing the causes which generated it. And the best proof for this is that the periodic motions, which we previously observed beyond our enclosure and which were due to this very gravitational field, have also ceased to exist."
The General Principle of Relativity declares, among other things, that whatever significance our mind may attribute to absolute motion, from the standpoint of experience the concept is meaningless, inasmuch as no observer would ever have means at his disposal to detect such motion. Thus the famous controversy between the geocentric and heliocentric hypotheses, over which the Founder almost lost his life, appears today as a futile quarrel about words. The two opinions are not two opposite horns of a dilemma, but two complementary aspects of a dialectic principle which by declaring absolute motion void of physical significance, reduces the choice between rest and motion to a mere matter of convenience in exposition.
The extraordinary precision of the formula which connects static force and acceleration has also lost its mystery. The relation is a tautology. Whether an observer is measuring force or measuring acceleration depends entirely on whether he is on the inside looking out or on the outside looking in. Indeed, the principle of relativity could be fittingly renamed principle of duality [D]. As such it is in consonance with that deeper duality which [Pg 104]pervades our consciousness and which permits man to view himself at will either as a part of the universe or as a thing apart from it.
Depending on the point of view—and this is quite in keeping with its relativistic character—one may hail the new doctrine [D] as the most magnificent achievement of the human spirit, or curse its advent as the dark hour when man was despoiled of the last vestige of a faith in a reality beyond himself.
The laws of nature [L] are drawn from experience, but to express them one needs a special language: for, ordinary language is too poor and too vague to express relations so subtle, so rich, so precise. Here then is the first reason why a physicist cannot dispense with mathematics [M]: it provides him with the one language he can speak . . . Who has taught us the true analogies, the profound analogies which the eyes do not see, but which reason can divine? It is the mathematical mind, which scorns content and clings to pure form.
Henri Poincaré, Analysis and Physics
FOR want of a better name, I shall designate as empirical principle that doctrine which elevates experience to the function of supreme arbiter of judgment, relegating to subsidiary positions all other agencies which in the past have guided man on his quest of truth. The principle does not proscribe speculation [S]; it does, however, prescribe its norms and circumscribe its scope, by imposing upon it proving grounds where the fruit of speculative thought are to be judged, and upon being judged approved or discarded. The laboratory or the observatory are these proving grounds, and, on occasion, the field, the factory, or the road. But wherever and however the test may be finally made, there is no appeal from its verdict. In short, the brain may be given full sway for a while, but, in the ultimate analysis, it is to the hand and to the eye that is left the last say in the matter. So does the doctrine declare.
Let us examine "empiria [E]" at work. Proceeding from results accumulated by experience, an investigator devises a rational scheme which aims at uniting under a single theory a maze of hitherto disconnected facts; now, inherent in the very process of ratiocination is the power to suggest facts other than those in [Pg 106]explanation of which the theory has been devised. Speculation rests, until these theoretical consequences of the rational scheme have also been tested. These tests may confirm the theory; however, more often than not discrepancies arise. Of course, there is the natural tendency to attribute these deviations from theory to errors of observation; so, no efforts are spared to eliminate these "errors" through refinement of experimental technique: more reliable instruments, more precise measurements. As a rule, this refinement ends in the recognition of the existence of a secondary phenomenon which the former experimenters, in their zeal to test the primary, have either neglected or ignored. Now, these secondary effects begin to press for an explanation.
To account for these discrepancies as well as for the new experimental facts, the original theory is discarded, or at least revised. The new theory, more general than the preceding, while accounting for the changed facts, also entails new consequences, which, in turn, must be confirmed by experiment, if the theory is to stand. So the process begins da capo, except that with each successive stage more ground is being gained.
How does mathematics fit in this general scheme of things? Is it just a convenient shorthand, a code, or at most a symbolic language, a sort of Esperanto of Science? That it serves as a powerful recording device cannot be denied; that thanks to its universal character it greatly facilitates scholarly intercourse, is just as patent. But do the functions of mathematics end here?
Now, to the extent that any language is used for precise statements, it, too, may be viewed as a system of symbols, as a sort of rhetorical algebra [A]. In this capacity a word is a symbol of a class or of a relation, a sentence but a logical proposition establishing a relation between classes. Yet, language is not limited to this purely logical function. In addition to being a symbol of a class of objects, the word has the capacity of invoking an image, the image of a typical object of the class, and in this way it carries a direct appeal to our senses. It is this dual function that makes language the link between logic and intuition.
As opposed to this, the mathematical symbol does not stand [Pg 107]for a single class, but for any one of a large group of classes subject to certain operations. It need not evoke in our mind a concrete object; in fact, it may have no concrete interpretation at all, or it may acquire such an interpretation long after all the rules of operations have been established, as was the case with the so-called imaginary quantities. Furthermore, a mathematical proposition is not judged true because it appears so to our intuition, or because it is substantiated by experiment: mathematical truth is but freedom from contradiction. This ultra-rational and, to all appearances, arbitrary criterion sets mathematics apart from science proper. There, we have seen, experience is regarded as the supreme arbiter of judgment, whereas mathematics strives to assign to experience the subordinate role of suggesting the truth, not judging it.
In spite of this intransigence, mathematics today occupies a dominant position within the physical sciences, and is slowly but surely invading the other fields of scientific endeavor. Why? Nothing could serve better to throw light on the nature of mathematics than an analysis of the causes of this persistent penetration. Let us begin with the more apparent causes.
Admittedly, mathematics is the ideal medium of ratiocination: its premises rest on logical foundations, and its entities lend themselves with the utmost ease to treatment by syllogism. Every one of the inexhaustible variety of mathematical forms is a complete and well-rounded rational discipline. The physicist has but to recognize in the law governing the phenomenon under observation one of these forms: not only will then the mathematical method permit him to give to his problem a rigorous formulation, but the sundry manipulations to which the form is subject will, when couched in physical terms, guide experiment into new channels.
Again, mathematics responds most readily to the incessant readjustment of experience and theory which is so characteristic of the empirical principle. Should, indeed, the secondary effects upset the serenity of the original theory, the mathematical form is there to adjust the discrepancies. For, nothing is as flexible and [Pg 108]as accommodating as this form: a change in the value of the constants which enter into the formula; the adjunction of a new term; and if these expedients fail to remove the difficulty, there are many other weapons in the arsenal of the mathematician reserved for just such emergencies.
But this does not exhaust the services which mathematics has rendered to the physical sciences. The very abstractness which vitiates mathematics as a medium for conveying ideas to the non professional, permits it to uncover kinships between phenomena which are so widely apart in content that they seem to possess nothing in common insofar as our sense-impressions are concerned. The electromagnetic theory is a case in point: here, three distinct disciplines—electricity, magnetism, and optics—were knit into a single theory after the laws governing these fields had been shown to conform to similar mathematical patterns.
If another phenomenon has previously been reduced to the same pattern which the phenomenon under observation obeys, the least that can be said about it is that there exists between these two phenomena a formal kinship. As a rule, an explanation is eventually found which exhibits a much more intrinsic kinship. Thus has the abstract character of the mathematical treatment led to the discovery of far-reaching relationships between phenomena altogether different in content, relations which physical intuition unaided could not have even suspected.
This unifying function of mathematics is further enhanced by what may be called its hierarchical structure; in the successive steps of its evolutionary process, the particular is being subordinated to the more general, thus forming an all-embracing hierarchy in which the rank of a concept is determined by its degree of generality. This structure is already apparent in the number [N] concept on which mathematics rests. It begins with the counting process and the integer; it ends with the notion of the general many-dimensional magnitude; this latter concept, however, includes the whole long road covered in the evolution, as well as the point of departure, the integer.
The same structure is exhibited in the fertile, and for applications most important, concept of function. The study commences [Pg 109]with the consideration of a simple proportion; it ends with the idea of the general function, which includes any relation representable by a table, the table consisting of two or more entries, or of an infinitude of entries, or of a construction so involved as to defy simple description; but in spite of this complexity, this definition still applies to the most elementary functions. Closely allied to function is the concept of equation: one commences with simple linear equation, and ends with intricate systems of differential equations, the solution of which may determine the status of a universe: yet here, too, the hierarchical structure is maintained throughout.
Because of this structure the mathematical method is ideally adapted to the monistic tendencies inherent in scientific determinism. Remember the Intellect of Laplace, who had condensed into a single formula the status of the universe? Well, among all intellectual activities of man, only mathematics possesses the potentialities of a scheme so sweeping that it may comprise the all, and still account for the any.
Thus does the mathematical method reflect the universe of discourse of science: a deterministic rational universe approachable through human experience. It is not surprising, therefore, that from a modest aid to experiment, mathematics has grown into the dominant idiom of theoretical physics [P].
Were the discussion to stop here, it would hardly cause any commotion in the camp of the physicist. He would, perhaps, resent the phraseology, preferring to express such thoughts in a language better adapted to his own outlook and vanity. Still, he would admit that the necessity of couching physical concepts in terms amenable to mathematical treatment has had an important bearing on the course of theoretical physics. But we cannot stop here; for, the influence of mathematics on the speculative aspects of the physical sciences is only a part of the story. At least as great, even if not as obvious, has been the influence which mathematics has exerted on the course of experimental physics.
Before any observation or experiment may begin, it is necessary to decide which of the numerous phases of the phenomenon will be observed, and lay plans for eliminating all other [Pg 110]phases. Now, it may seem that this choice is entirely in the hands of the observer; but, in point of fact, the experimenter has little latitude in the matter: the choice is determined in part by the type of apparatus and instruments at his disposal, in part by the methodology which he has acquired during his training period, but most of all by his habits of thought.
Consider the equipment: in the course of the last hundred years, instrumental technique has made enormous strides, and the trend has been in the direction of greater precision of measurements. This is reflected in the very names of the instruments: what used to end in "scope," now ends in "meter"; i.e., while in former days the apparatus was used chiefly as a means of detecting a phenomenon, today the dominant tendency is to reduce the phenomenon to number. Relentless elimination of those aspects of a phenomenon which are irreducible to number and may for this reason be called qualitative; gradual transformation of others more amenable in this regard to entities susceptible of mathematical treatment, as evidenced in the evolution of such concepts as heat, color, or sound—this has been the history of experimental physics. Here the imprint left by mathematics is evident enough.
But the same is true of the experimenter himself: it is easier, indeed, for a camel to pass through a needle's eye, than for a scientist to depart from scientific precedent, and the precedent has been to place greater and greater reliance on the mathematical method which has conferred so many benefits on the physical sciences. The result is that the modern physicist identifies the study of any phenomenon with the determination of the mathematical law which governs it. The qualitative phases of the phenomenon, because of their mathematical "inarticulacy," are sidetracked as much as possible.
The orthodox physicist would, no doubt, indignantly reject this thesis; deny that he is being spurred on by any other consideration than the search for facts; insist that the mathematical processes used by him are but means to an end, convenient recording devices, or tools at most. Well, it seems to me from where I sit that one may aptly apply here the wisecrack of the car [Pg 111]driver: "You commence by running the thing, you finish by it running you."
One curious aspect of this mathematical penetration is the equanimity with which it is met not only by those whose preserves are so insidiously invaded, but by philosophers.
It has not always been so. The mathematization of human knowledge is almost as old as mathematics itself. The Pythagorean dictum "Number rules the universe" found many adepts among the thinkers of Ancient Greece. Still there was no lack of opposition. In the days of Plato [P] loud protests against such views were voiced by philosophers of the Eleatic school of which Parmenides and Zeno [Z] were brilliant representatives.
In the middle of the seventeenth century, a protest against this mathematization was lodged by no less a person than Blaise Pascal, who in the earlier part of his career had contributed so much to mathematics. A miraculous escape from a runaway team turned his mind towards loftier subjects; in the course of time he had come to repent his earlier achievements; ridiculing the idea that the world, permeated as it was by the mystic presence of God, could be reduced to number and extension, he heaped contempt on his former confrères: "Mathematicians," he wrote, "are never subtle, for the subtle never cultivate mathematics."
His was a voice lost in the desert. Within less than a century his own contributions and those of his contemporaries blossomed forth into the Differential and Integral Calculus. A veritable orgy of applications followed, an orgy which far from being censured by the thinkers of the period, led to such ecstatic comments as that of Voltaire [V]: "This method of subjecting the infinite to algebraic manipulations is called differential and integral calculus. It is the art of numbering and measuring with precision things the existence of which we cannot even conceive. Indeed, would you not think that you are being laughed at, when told that there are lines infinitely great which form infinitely small angles? Or that a line which is straight so long as it is finite would, by changing its direction infinitely little, become an infinite curve? Or that there are infinite squares, infinite cubes, and infinities of infinities, [Pg 112]one greater than another, and that, as compared with the ultimate infinitude, those which precede it are as nought. All these things at first appear as excess of frenzy; yet, they bespeak the great scope and subtlety of the human spirit, for they have led to the discovery of truths hitherto undreamt of."
Eventually, the reaction did set in. There arose the irrepressible Berkeley [B] to voice his protests against the use of infinitesimals, "these ghosts of departed quantities," as he called them. But the Bishop's lamentations went for the most part unheeded. So did the aesthetic arguments of Goethe [G], directed against the mathematical optics of Newton and his color theory. "The mathematician," he wrote, and he meant the physicist too, for, he made no clearcut distinction between the two species: "is like a Frenchman, you tell him a thing, he translates it into his own language, and behold it is something entirely different."
It was a lost cause that these thinkers were defending, and it was recognized as such by the clairvoyant Nietzsche [N]. He, too, waxed indignant at times: "In mathematics," he wrote, "there is no understanding. In mathematics there are only necessities, laws of existence, invariant relationships. Thus any mathematico-mechanistic outlook must, in the last analysis, waive all understanding. For, we only understand when we know the motives; where there are no motives, all understanding ceases." Yet he cherished no illusions as to the eventual outcome of this perpetual counterfeiting of the world by number: "The movement," he wrote in his diary of 1876, "will end with the creation of a system of signs; it will end with waiving all pretenses to understanding; nay, in renouncing the very concept of cause and effect." And, unlike his predecessors, he refused to view the movement as but a passing vogue of an age intoxicated with progress. He firmly held that this relentless reduction to number had been predicated by the very structure of the human mind.
This then is the first condition of objectivity: what is objective must be common to several minds, and, by the same token, can be conveyed by one mind to another; and since such transmission cannot be brought about in any other way than by the "discourse" which inspires so much defiance in M. le Roy, we are forced to conclude: No discourse, no objectivity.
Henri Poincaré, Science and Reality [R]
THE German mathematician and logician Gottlob Frege, one of the keenest intellects of recent times, once wrote: "That remote ancestor of ours to whom it had first occurred that it was one and the same sun that rose on successive mornings, and not a different sun each time, made the first great scientific discovery." One could extend this remark to include all sensory experience.
I look out of the window and perceive a tree. When analyzed more closely, this perception resolves into a number of more elementary sensations; when these latter are juxtaposed, they are found to be not only disparate, but conflicting. Still, by some selective process which is the more remarkable as it seems altogether automatic, my mind accepts some of these sensations as true, rejects others as mere appearances, and finishes by reintegrating the whole complex into a single impression which it conceives as emanating from a unique object of the external world: the tree. At another time, I may be confronted with another complex of sensations quite distinct from the former: still, my mind by some automatic process of adjustment identifies this new complex with the former, attributing it to the same external object: the tree. That it is the same tree that I perceive every time I look out of the window, and not a different tree each time, [Pg 114]therein lies the clue to the possibility of knowledge, for, were it not for this coordinating and integrating faculty of my mind, the world which impinges on my senses would appear to me not as a universe, but as a fleeting chaotic smudge.
The role of the mind in coordinating those impressions which are susceptible of quantitative formulation is even more striking. A case in point is the size of an object. We judge it largely by our senses of vision and touch, and all of us place greater reliance on these two senses than on all the others combined. Still, we are all aware of the many serious discrepancies to which even these more reliable senses are subject. I am not referring here to the discrepancies between the judgments of different observers; for the purpose at hand we may confine our considerations to a single individual. Thus one's visual estimate of the size of an object depends not only on proximity, on the angle from which it is viewed, on illumination and other external conditions, but also on the voluntary or involuntary changes in the disposition of the observer's eyes. The tactile sense displays these uncertainties even to a greater degree.
How little reliance can be placed on these direct perceptions was forcefully brought home to me some years ago, when I was attending a dinner of executives and engineers of a large ball bearing corporation. Some practical joker produced a steel ball and passed it among those present with the request that each of us record his estimate on a card provided for the occasion. Now, most of those present had been handling steel balls for a great number of years; still, the estimates ran all the way from 7/8 of an inch to 1 inch and a quarter, and even the average estimate departed substantially from the measured value, which, we were informed later, was one inch in diameter.
The more one ponders over these matters the more one comes to doubt the very possibility of organized knowledge, let alone of those sciences, known as exact, which are entirely committed to quantitative methods. Yet, it is precisely these sciences that have made the greatest strides in modern times. The situation is well nigh paradoxical: on the one hand, these sciences are [Pg 115]pledged to quantity as to a sine qua non; and, on the other hand, they profess not to depart a single iota from the empirical principle which invests experience with the function of supreme arbiter, from whose decision there is no appeal.
The clue to this enigma is to be found in the interpretation of a term. What is this experience which the scientist so reverently invokes on every step? Could he be speaking of the experiences conveyed to him by his own senses, this many-headed hydra, each of many tongues, each tongue vociferously screaming its own claim, and as vociferously disputing the claims of all other tongues? Is this confusion of tongues the scientist's supreme arbiter and last court of appeal?
No, indeed! The experiences which the physicist has in mind resembles this incoherent and inarticulate experience of his senses no more than does this blue streak on your map resemble the turbulent Niagara, or the temperature chart of a patient the delirium of his feverish brain. What the physicist deals in is a sort of sublimated [S] experience. He thinks not in terms of his human sensations, but of the laboratory which houses his instruments of precision. Here delicate gauges have replaced his halting touch, lenses and mirrors his shifting vision, chemical balances his odor and taste, vacuum tubes his imperfect hearing, a column of mercury his crude skin, which cannot even distinguish between extreme heat and extreme cold. Here, in his laboratory, his stuttering judgment is incessantly prompted by graduated scales and dials; here, there is harmony instead of conflict, for here everything has been designed according to a preconceived plan.
Not the frail body of man, not his muscles and skin and blood and nerves, which are at the mercy of all the vagaries his flesh is heir to: the theatre of this sublimated experience in this battery of instruments which despite their complexity agree with each other, and agree with the universe of discourse which has produced them. It is a species of Faustian Homunculus [H], a gigantic automaton, designed to replace the fickle sensations of man. Its arms are of steel, its eyes of glass, its lungs of rubber, and mercury flows through its veins; it is armed with pointers and styli [Pg 116]which play on graduated scales and dials and revolving drums, registering and recording this sublimated experience for which experimental evidence is another name.
The robot is far from complete, but the plans and specifications are ready. They have always been ready, ever since that instant when it has dawned upon man that the "true" world is not that fleeting confusion disclosed by his senses, but a universe of harmony and order, even as his mind reveals it; a universe in which neither ambiguity nor contradiction are possible, in which no measure can have more than one value at any one time; a universe, in short, in which mathematics and causality reign supreme.
If there ever was such an instant, the future of experimental science was sealed then and there. To discard direct perception as a source of knowledge, to create a new experience which fits the universe preconceived by man's mind, to invest this sublimated experience with the power of dictator of judgment—such has been the relentless trend of experimental science up to the present day. May I be so bold as to express the belief that this trend will continue unabated as long as experimental science will exist?
One arrives at this grandiose scheme through a purging process which aims at liberating experimental judgment from the ambiguities inherent in man's senses. Drastic this process certainly is; and yet, as we shall presently see, it does not go far enough. An incongruity still remains which has the potentiality of wrecking the whole plan, by vitiating the application of mathematics to this sublimated experience.
To bring out this point, I shall ask the reader to imagine that he has been presented with a number of steel bars, identical except for their lengths. To fix ideas, let us assume that these have been carefully measured in the laboratory and found to range from 30 to 50 millimeters; in particular, three of these bars, marked A, B, and C, measure 30, 31, and 32 mm. respectively. Of this, however, you know nothing; nor do you want to know, since this information may prejudice your judgment; for, [Pg 117]you aim at ascertaining what sort of measuring technique one could develop with one's senses unaided.
You commence by laying the bars, A and B, side by side: you find that neither your eye nor your fingertips can discern any difference between the lengths of these bars; so you declare them identical. You repeat the same comparative test with B and C; you decide that these two bars are also identical in length. Next you juxtapose A and C: but now both your eyes and your fingertips can clearly discern that C is longer than A. You arrive at the conclusion that two things may be identical with a third thing, without being identical to each other.
But this conclusion stands in direct contradiction with one of the most important axioms of mathematics, TRANSITIVITY [T], which asserts that two quantities equal to a third are necessarily equal to each other. This axiom is back of most of the operations of arithmetic; without it we could neither transform identities nor solve equations. I should not go so far as to say that a mathematics denying transitivity could not be constructed. The important fact is that the physicist uses no such modernistic discipline, but the classical mathematics of which this axiom is a cornerstone.
What gives him the right to do this? Could it be that the introduction of scientific measuring devices in lieu of direct perception has removed the contradiction? No. Reading a graduated scale is the ultimate goal of any measuring device; consequently, however ingenious may be the designer of the instrument, he must, in the last analysis, rely on the senses of some observer, more particularly on vision. When, on the other hand, we examine more closely the operation of reading a scale, we find that it does not differ in any essential feature from the hypothetical case of the bars considered above. To be sure, the critical interval which in that case was one millimeter, may now have been contracted to one micron; through amplification, and by rendering the measuring devices more sensitive, one may even succeed in reducing the interval to a small fraction of a micron. And yet, it is obvious enough that no matter how far this process of refinement be carried, it cannot eliminate our difficulty, nor even [Pg 118]minimize it; for, in the end data must remain of which one could say: "I find measure A identical with measure B; I also find measure C to be identical with B; still I can clearly discern that C is greater than A."
We thus reach the startling conclusion that inherent in the very process of reading a graduated scale there is a circumstance that vitiates the application of mathematics to the results of this reading [M]. Nonetheless, experimental physicists, having recorded these data, proceed to add them, multiply them, apply general mathematical processes to them; they regiment the results into functional relations; they solve the equations suggested by these relations, interpreting the solutions as potential readings of some instrument, even if the quantities thus obtained fall within the critical interval of the instrument. In short, they proceed as though these data, to which even the first axiom of mathematics fails to apply, were bona fide numbers [N] which obey unreservedly all the principles of mathematical decorum.
Moreover, the nonchalance and self-assurance with which they go about this calculating business are ample evidence that no doubts ever cloud the serenity of their outlook. Indeed, their faith in the absolute validity of mathematics may be envied by many a modern mathematician who, unlike his classical predecessor, has learned the meaning of qualms. Should you ask the physicist how he can possibly maintain this faith in the teeth of the obvious incongruities inherent in the reading of his scales, he would, I imagine, answer:
"I am a practical man, and your so-called incongruities appear to me as so much hair-splitting. At any rate, they are irrelevant to the issues which concern me as a physicist. You have catalogued a number of physiological limitations common to all men. Well, I am not physiologist. The field of my activities is the objective universe, which is entirely independent of sensations and observations, and certainly is not affected by these incongruities. The phenomena of this objective universe do obey precise mathematical laws; the variable magnitudes which characterize these phenomena do not change in the jumpy, jerky fashion which you have described, but vary in a continuous manner; they [Pg 119]flow in a gapless stream, as it were. That no graduated scale can adequately represent such a gapless stream is readily granted. But from this by no means follows that we must reject the readings of these scales; what does follow is that we must view them as mere approximations to the true objective measurements of the magnitudes in question. These objective measurements, however, are bona fide numbers, since they satisfy the most exacting mathematical requirements. It is these numbers that the physicist has in mind when he sets up his mathematical formulae and equations, and not the readings of his instruments which serve as mere indications of the true state of affairs."
Interrupt him long enough to remark that he had begun by emphasizing that he was a practical man, and finished by invoking ideal magnitudes which were admittedly inaccessible to his instruments and were, therefore, outside his jurisdiction as an experimentalist—and he would counter:
"I dislike the term 'ideal' as applied to these objective magnitudes. Inaccessible to our direct sense perception they undoubtedly are, but not ideal in the sense that they are unreal. On the contrary, the objective universe which they measure is the one and only reality, whereas the data furnished by our senses and their extensions, the scientific measuring instruments, are mere appearances, and would be indeed worthless were it not for the fact that they approximate this objective reality.
"You ask how I know this. Well, I shall admit from the outset that I could not prove this contention by means of the canons of formal logic, and that an experimental proof is also out of question. Thus, the existence of this objective universe must be viewed as an assumption. This assumption, however, is more than justified on pragmatic grounds, since the alternative, as your own analysis of sensations has amply shown, leads to the denial of the possibility of knowledge.
"But there is still another argument, and one that should appeal to a mathematician. The evolution of experimental physics has not been haphazard: the trend has been in the direction of greater and greater precision. This may be exhibited by the history of any physical constant. If the various values which [Pg 120]at one time or another have been attributed to such a constant be put in chronological order, the set so obtained would have all the earmarks of what the mathematician is pleased to call a convergent sequence. A limiting value is being approached, and what could this limit be if not the true value of this particular constant? The discrepancy between the limit and the observed values becomes more and more insignificant with the refinement of instrumental technique, and should this trend continue in the future—and there is no reason why it should not—the discrepancy would eventually become less than any number assigned in advance. To be sure, the true value must forever remain inaccessible to man, inasmuch as it is the consummation of an infinite process. On the other hand, does not the mathematician constantly deal with the limits of such processes, processes that admittedly cannot be consummated in a finite number of steps? What is sauce for the goose is sauce for the gander!"
And here we have reached an issue which is of vital concern to mathematics itself. For, the mathematician, too, deals with two species of things, so different in character as to appear mutually exclusive. There are, on the one hand, the discrete collections, typified by the sequence of natural numbers, 1,2,3,4, . . . , with which all mathematics begins. There are, on the other hand, the continuous aggregates, which derive from our intuition of time.
To develop procedures which would permit one to pass with facility and rigor from the discrete to the continuous and back—such has been the goal of mathematical analysis [A]. The result achieved is one of the great triumphs of the human spirit. How has this success been brought about? The answer implies a conception which I have touched upon on several occasions in these essays, the conception of infinity [I]. I must now undertake a more thorough analysis of this conception in the hope that it may shed light on some of the perplexing questions raised by the preceding discussion.
Why then does this judgment force itself upon us with such an irresistible force? Because it is only the affirmation of the power of the mind which knows itself capable of conceiving the indefinite repetition of the same act when this act is possible at all. . . .
Henri Poincaré, On the Nature of Mathematical Reasoning
THE theme of this chapter is the Infinite [I]. What place should be assigned to the concept among the other tenets which have guided man on his journey from primitive lore to the present-day integrated outlook on the universe? I waive the futile controversy between mathematicians and philosophers which began in the days of Plato and will end when the last thinker will be laid to rest. It is in the light of human values that I want to appraise its genesis and growth.
Long before science had an independent existence, in those remote ages when it was a mere echo of religious speculation [S], and when mathematics was confined to crude surveying and cruder-yet numerology—the priest-philosophers of the Orient had already meditated on the infinite. These meditations have left an indelible imprint on modern religions. Infinitude as a Divine Attribute is a feature of all advanced creeds, however these may differ in other respects. Closely allied to such other ideas as omnipotence, omniscience, omnipresence and eternity, it pervades all doctrines and all mythologies, monotheistic and pagan alike.
Is this similarity between religious and scientific speculations on the infinite accidental? Is it just another manifestation of the inadequacy of language which causes the same term to be used in [Pg 122]two distinct and unrelated senses? Or is it an indication of the common source from which religion and science emerged?
Be it an axiom or a definition in disguise, an expression of man's impotence to exhaust the universe by number, or that of his innate conviction that what has been said or done once can ever be repeated—the infinite permeates the elaborate edifice of mathematics. From it mathematics derives its power, its dominant position among the other sciences. The generality of mathematical laws, the inexhaustible variety of mathematical forms, their flexibility and susceptibility to manipulation, the hierarchical character of the mathematical structure, in short, all the features which makes of mathematics the model and the idiom of exact sciences may be directly or indirectly traced to the infinite.
We encounter the concept on the very threshold of mathematics. As we advance, we meet, with every step, more and more extensive applications of the idea, until we reach infinitesimal analysis, where the infinite process reigns supreme. We advance still further and come to the theory of aggregates, when we begin to realize that there are infinities and infinities, that the natural sequence, 1, 2, 3, . . . , while infinite, is not infinite in the same sense as the totality of points on a line. We finally attain the dizzy heights of the transfinite [T], where this distinction between the various infinities serves as point of departure of a new arithmetic.
Yes, mathematics owes to the infinite its greatest triumphs. Alas! The concept has been also the source of its greatest perplexities, the box of Pandora from which have issued the many paradoxes, antinomies, and logical difficulties which have harassed mathematicians since the days of the Sophists. These difficulties begin with counting; as we encompass the field of modern mathematics, they become more serious; and yet the growth is in extent rather than in essence. For, like counting itself, of which the infinite process is but an extension, it stands or falls according as we concede or refute the statement that what has been said or done once can ever be repeated.
The prototype of the infinite process is iteration [I], an indefinite [Pg 123]chain of identical operations, each step of which is being applied to the result of the preceding. The counting process itself is such an iteration: here the generating operation is addition of 1, and the result is the natural sequence of numbers: 1, 2, 3, . . . The first term of this sequence is 1; there is no last, for any term, however large, has a successor. We mean precisely this when we say that a sequence is infinite.
Another form of iteration [I] is what the Greeks called dichotomy. Here the generating operation is division by 2: the sequence generated by this process is the geometric progression: 1, 1/2, 1/4, . . . Like the natural sequence, this progression has no last term; unlike that sequence, its terms decrease indefinitely in magnitude. The mathematician expresses this fact by saying that the sequence converges towards 0 as a limit.
Any number, whether integer or fraction, may be viewed as the limit [L] of some infinite process, and, as a matter of fact, of an infinite variety of such processes. Take the infinite sequence of fractions, the numerators of which, as well as the denominators, increase in arithmetic progression, and designate the differences of the two progressions by p and q, respectively. Then, no matter what fraction we choose for first term, the sequence will always converge towards the fraction, p/q. To illustrate: the sequence 1/2, 4/6, 7/10, 10/14, 13/18, 16/22, 19/26, 22/30, 25/34, . . . converges towards the fraction 3/4.
Integers and fractions, whether positive, negative, or zero, are classed by the mathematician under the collective name rational number. Again, if an operation, process, or sequence involves only the four fundamental operations of arithmetic, then it is called rational. The examples of the preceding section involved such rational processes; moreover, their limits, too, were rational numbers. The question arises whether this is generally the case; i.e., whether any rational sequence which does converge at all converges towards a rational limit.
It would appear at first sight that the answer should be in the affirmative: for, is it not true that no matter how far such a process be carried, only rational numbers emerge? And yet, far from this being the case, infinite sequences of rational numbers [Pg 124]constitute the source of a vast aggregate of mathematical entities which cannot be represented by rational numbers, and are, for this reason, called irrational. Quadratic and cubic roots, the number π, logarithms and trigonometric ratios are examples of such irrational numbers. The infinite processes which generate these irrationals are the very same used to obtain rational approximations to these numbers, such as are recorded in tables.
If we agree to call any number which is the limit of some rational sequence a real number [R], we can express the state of affairs by saying that not every real number is rational, even if every rational number is real. Moreover, in a certain sense, on which I cannot elaborate here, the rational numbers constitute but an infinitesimal drop in an infinitely vast ocean of real numbers.
Now, the fact that we can generate non-rational numbers by applying infinite processes to rational numbers raises the hope that the same procedure when applied to real numbers would generate a new variety of mathematical entities. Such, however, is not the case. Georg Cantor, to whom we owe most of these developments, proved that whatever may be accomplished by applying infinite processes to real numbers could be done by operating upon rational numbers alone. In other words, the domain of real numbers contains all of its own limits: this remarkable fact is sometimes expressed in the statement that the domain of real numbers is closed. As opposed to this, the aggregate of rational numbers may be viewed as "wide open," inasmuch as it does not contain all of its own limits.
This property of closure endows real numbers with a completeness which rational numbers do not possess. It suggests that the domains of real numbers and of conceivable numbers are identical, and from this there is but a step to regarding the domain of real numbers as a continuum, classing it, as it were, with such aggregates as the totality of instants in duration, or the totality of points on a line.
The hypothesis that it is possible to establish a complete and reciprocal correspondence between the points on a line, on the one hand, and the real numbers, on the other, is known to [Pg 125]mathematicians as the Cantor-Dedekind axiom [C]. This designation is misleading, for, this axiom lies at the foundation of analytical geometry, a discipline which preceded the two mathematicians after whom the axiom is named by at least 250 years. I say at least, for, while analytical geometry in systematic treatment is the creation of Fermat and Descartes, the fundamental aspect of the axiom, i.e., the relation which it establishes between extension and number, is implicit in the theory of proportions as treated in the Elements of Euclid.
To justify this axiom, let us agree to call the aggregate of all points on a line a linear continuum [C]. What structure does our intuition assign to this continuum? In the first place, the line extends as indefinitely in one sense as in the other; in the second place, between any two points an infinitude of other points may be found, and this no matter how close the two points may be; in the third place, we may imagine all sorts of operations which, starting with some points on the line culminate in others; we can further imagine infinite processes composed of such operations; they may be divergent or convergent; if, however, they do converge, their limiting points also belong to the line.
All these properties have their counterparts in the arithmetic of real numbers: the aggregate of real numbers possesses no last term, neither has it a first; between any two real numbers, however small be their difference, an infinitude of other real numbers may be inserted; all potential limits of convergent processes operating on real numbers are themselves real numbers. Thus, it would seem that one is justified in interpreting the totality of real numbers as a bona fide continuum, the arithmetic continuum.
And yet on closer analysis the analogy between the linear and the arithmetic continua is not convincing. Indeed, our ideas of continuity derive from our intuition of time. As a consequence, we conceive a continuum as a gaplass stream. When, for instance, we speak of the continuous motion of a particle along a straight line, we conceive that in passing from position A to position B all the points of the segment AB have been traversed by the particle. In other words, here is a "mechanical" procedure by which we can [Pg 126]account with a single stroke for all the elements of a continuous portion of our aggregate. What is the arithmetical counterpart of this procedure? By what possible process can we generate all the real numbers contained, say, in the interval between 0 and 1? We could systematize our task by agreeing to express any number as a decimal fraction, finite or infinite; then, our problem would be to write down all proper decimal fractions, a godlike task to say the least, since we are unable to put down even one of these infinite fractions.
How could one counter this difficulty? Only by invoking the aid of a supermind, a sort of Laplacian Intellect, conversant with all the infinite processes and all their limits. And when I say all, I mean not only processes which are known to us or are derivable from those known to us, but all hypothetical processes which we glibly lump into one class under the elusive title of conceivable. To this supreme intellect all these processes would be as cogent as the operation of adding one is to us; all the potential limits of these processes would be at his command, to classify, to group, and to order at will. So let us entrust this intellect with the task of arranging the real numbers in order of magnitude; the aggregate so obtained, extending from negative infinity to positive infinity, and embracing all real numbers, is the arithmetic continuum. And now, before we dismiss this supermind, we may as well ask him to label all the points of a straight line by means of these real numbers, very much as though these points were beads on a string. Then this complete and reciprocal correspondence between the arithmetic of real numbers and the geometry on a line would be consummated.
Let us now return to the discussion of the preceding chapter, interrupted by this excursion into the subtleties of the infinite.
Consider any scientific instrument—say, a thermometer, pressure gauge, micrometer, protractor, voltmeter or interferometer. Whatever the physicist may be measuring, he is measuring by means of a graduated scale; this scale is calibrated, its sundry divisions stand for integral values of the chosen unit; the subdivisions of the scale indicate rational fractions of the unit. The experimenter records the observed data in rational numbers, [Pg 127]he adjusts his observations by means of rational operations. He uses neither infinite processes, nor irrationals of any kind; for, even if his computations involve such quantities as √2 or π, he promptly replaces these by some rational approximations, and gives them no second thought. In short, rational arithmetic alone enters into this phase of his work; and were the collecting of data his sole object, he could heartily subscribe to a program which would bar from mathematics infinite processes altogether.
However, science is not limited to collecting data: the latter is but a means to an end, the end being the determination of the laws governing the phenomenon of which the data are manifestations. When recorded on a sheet of graphing paper, these data appear as a series of disjointed dots. The investigator connects these dots by continuous arcs, filling the gaps as it were. This procedure is known as interpolation. As a rule, the scientist goes even further: if the curve has "ugly" corners, he obliterates these, too, on the ground that such irregularities are due to errors of observation. For, natura non facit saltus, so there is no more reason for the rate of change of a phenomenon to be discontinuous than there is for the data themselves.
What the physicist implicitly assumes is that all the possible values of the variables under his observation constitute a continuum; that the phenomenon obeys a sort of Cantor-Dedekind axiom; that to any possible state corresponds a real number, and to every real number within the observed range corresponds a physical state. On the basis of these assumptions, he reduces his problem to differential equations, determines the solutions of these equations in terms of continuous functions; differentiates and integrates these latter, deriving new functions; these, in turn, lead to new relations which he regards as logical consequences of his original formulation, as part and parcel of the phenomenon under observation. When the time arrives to verify these consequences experimentally, he again uses rational approximations only, forgetting in his zeal the elaborate scaffold which he has used in transit.
Thus while in his actual work the physicist may deal only with finite decimal fractions, he assumes that what he is measuring constitutes a continuum. For were it not a continuum, he [Pg 128]could not apply the theorems of mathematical analysis to the results of his measurements, and if he could not apply analysis to his measurements, he could not connect these results by mathematical laws, or express his ideas in mathematical terms.
It may be argued, that the mathematical apparatus which we call infinitesimal analysis, while a great convenience, is not a necessity, inasmuch as the progress of mathematics in the last fifty years has been in the direction of extending the operations of analysis to aggregates other than continua. And so it is not inconceivable that at some future date the mathematician will be able to present the physicist with a workable apparatus free from the difficulties incident to continuous functions. Such a "rationalization" of mathematics would erase the conflict between the two aspects of the scientist's work, the experimental and the speculative: from then on, all the mathematics which the physicist uses would involve only rational operations on rational numbers. A reign of reason should follow, for have not all the difficulties been removed at the source?
The answer is no: even rational arithmetic [A] depends on the conception of infinity. Indeed, one cannot as much as add up one's grocery bill without invoking the concept of infinity. And if you think that this is an exaggeration, try to give yourselves account as to the logical grounds of the operations of addition and multiplication which you so glibly perform. Try to demonstrate that the sum is independent of the order of the terms; that in order to add three numbers you may proceed in one of two ways: either add the third to the sum of the first two, or else add to the first the sum of the last two; that similar properties hold true for multiplication; that in order to multiply the sum of two numbers by a third you may compute the individual products and add the results. You will recognize that on these propositions depends the validity of the arithmetical rules which you learned before you were ten years old; so I shall ask you to bear with me while I outline the principle involved in their demonstration.
"There is, we must admit, a striking analogy between this and the usual procedure of induction. But there is an essential difference. Induction, as applied in the physical sciences, is always uncertain, because it rests on the belief in a general order in the universe, an order outside of us. On the contrary, mathematical induction, i.e., demonstration by recurrence, imposes itself as a necessity, because it is only a property of the mind itself. . . ."
"We can ascend only by mathematical induction, which alone can teach us something new. Without the aid of this induction, different from physical induction but just as fertile, deduction would be powerless to create science."
Henri Poincaré, On the Nature of Mathematical Reasoning
THE principle known as mathematical [I] or complete induction, applies to any ordered sequence of terms, and may be loosely put in the statement: what is true for the first term of a sequence is true for all terms [I], provided that if true for some term it is true for the next. I shall illustrate its application on the following theorem: If any number, say n, of consecutive odd integers beginning with 1 be added, the resulting sum is a perfect square, namely n2. Thus: 1 + 3 + 5 + 7 + 9 = 25 = 52.
The proposition is certainly true for n = 1, because it leads to 1 = 12 which is a tautology. Suppose, then, that we have verified the property for some number n = p, and found that
1 + 3 + 5 + 7 + . . . + (2p - 1) = p2.
Does it hold for n = p + 1? Let us add the next odd integer, namely, 2p + 1, to both sides of this equality; the right side becomes: [Pg 130]p2 + 2p + 1, and this is identical with (p + 1)2. Thus it is sufficient to assume the theorem true for n = p to have its truth for n = p + 1 follow as a logical necessity. But we know that the proposition is true for n = 1, it must, therefore, be true for n = 2; and if true for n = 2, it must, by the same token, be true for n = 3. Continuing in this manner, we conclude that the proposition is generally true.
Let us return to the fundamental properties of the operations of arithmetic. These are known as commutativity, associativity and distributivity. How are these properties proved? By mathematical induction, the very same procedure which I have illustrated on the example above. In fact, it is only because the details of the demonstrations are more elaborate that I have chosen the more simple proposition.
"Granted," the reader will counter: "but what has this to do with the infinite? Where is the connection between this principle which you are pleased to call mathematical induction and the conception that every number has a successor?" The answer is that while complete induction is applicable to finite collections as well as to the infinite, in the former case it is superfluous, since any property of a finite collection can be proved by "incomplete" induction, i.e., by direct verification. If, for instance, I assert that the fifth power of any number ends in the same digit as the number itself, I could prove this contention by mathematical induction. However, I could also prove it by direct substitution.
When, however, one is confronted with an infinite collection, its very inexhaustibility precludes any such direct attack. To demonstrate that such and such a property is universally true, generally true, true for all members of an infinite collection, one must have recourse to a procedure which is not only not vitiated by the inexhaustible character of the collection, but which derives from this inexhaustibility its very life. The principle of mathematical induction is such a procedure; what is more, it is the only such procedure, for, in the last analysis, any mathematical method of demonstration applicable to infinite aggregates is but complete induction, either overt or disguised. This will not appear [Pg 131]surprising if we reflect that all that is required of a collection to which mathematical induction is applicable is that any term should have a successor, which is but another way of saying that the collection be infinite.
The term mathematical induction, as applied to the fertile procedure just described, has been often criticized as inadequate, and even misleading, because the only thing that smacks of induction here is the verification that the property in question holds for the first element of the collection. This step, while indispensable, is not the salient feature of the method; what is characteristic of the principle is reasoning by recurrence, the passage from predecessor to successor, the hereditary step, to use a term coined by Bertrand Russell [R]; and this step has nothing in common with the inductive methods employed in experimental sciences.
To be sure, the experimenter, too, deals at times with aggregates which, while not inexhaustible in the mathematical sense of the word, are so vast that a direct verification in each individual case is not only impractical but, as a rule, impossible. To cope with this difficulty, rules have been devised which are known under the collective name of induction.
I shall illustrate this on this very simple assertion: the sun will rise tomorrow. This statement contains as great a degree of certainty as may be conceived outside of mathematics. Whence does it derive this certainty? Well, in our own experience and in that of our forebears, the sun has ever risen with periodic constancy. The single exception occurred when Yahweh at the request of Joshua stopped the sun for a day so that his chosen people might consummate their orgy of blood. And even here the Scripture hastens to add that there was no day like it before or after it.
The argument back of that statement, or of any similar statement, is known as inductive inference [I]. In the words of David Hume [H], it rests on our belief that the future will resemble the past. Thus, if in the observation of any phenomenon a certain tendency towards permanence has been exhibited, then it may be inferred with reasonable safety that the same tendency will manifest itself [Pg 132]in the future, the certainty of the inference being the greater the more frequently the tendency has been observed in the past. This principle is of inestimable value to the experimental sciences; and this is hardly putting it strongly enough, inasmuch as inductive inference is our one "rational" clue to the future. It is not only the basis of all our planning and activity, but the fountainhead of experience itself.
I should like to emphasize the kinship between these two principles: mathematical induction and inductive inference.
Of these, the first applies to infinite mathematical collections, while the second implies a series of recurrent events which, because of the indefiniteness of the future before us, has all the earmarks of an inexhaustible collection. Whenever we apply inductive inference to such a temporal series, we say in substance: "Never, to our knowledge, has this event occurred but that it has occurred in the next case on record. It is reasonable to infer, therefore, that the same invariable succession will manifest itself in the future." When the argument is paraphrased in this manner, its resemblance to reasoning by recurrence becomes overwhelming.
In a certain sense the two principles complement each other. Mathematical induction, by sanctioning indefinite iteration, affirms the power of the human mind to conceive the endless repetition of any act that is at all possible; inductive inference, on the other hand, reassures us that this power is not idle fancy or vain mania of grandeur, inasmuch as Nature itself is bent on such an indefinite repetition of identical events.
Both principles are intimately related to number. Mathematical induction lends to number, and through number to all mathematics, that exceptionless generality which no other domain of human knowledge possesses. Induction by inference invests number with the dignity of supreme arbiter of judgment by maintaining that an event which has occurred a great number of times cannot be classed as a sheer accident; that this recurrence points to a universal law, to a certainty; that this certainty could be established in full rigor experimentally, were we not by our physical [Pg 133]and physiological limitations prevented from observing the phenomenon an infinite number of times.
The function of the infinite in mathematics is twofold: first, in the guise of complete induction it endows the laws of rational arithmetic with utmost generality; second, the infinite processes, in generating the arithmetic continuum "bridge" the chasm which exists between the idea of a discrete collection inherent in our number concept and our time-intuition which conceives duration as a gapless stream.
Since then mathematics derives its validity from the infinite processes, it is natural to inquire, whence does the infinite derive its own validity. That it is an axiom will be readily granted. But then there are axioms and axioms: some are but canons of logic, others are vouchsafed by experience. The conception of infinity belongs to neither category. That it is not a consequence of formal logic is attested by the many logical paradoxes which it has engendered, while the essentially finite character of all human experience precludes the possibility of its deriving from that source.
There is still a third category of principles which have played a most fundamental part in the evolution of scientific thought. They bear a striking resemblance to religious credos, and may, for this reason, be called articles of faith. To this category belongs our beliefs in the absolute character of space and time, in the causal connection between events, in the rational pattern of the universe, and many other irrefutable tenets. What is more, the more irrefutable a tenet appears to our mind, the greater our right to suspect it of belonging to this category of articles of faith.
Here, in my opinion, belongs the conception of infinity, too. From the possibility of an act in a finite number of cases we infer its possibility in an indefinite and unlimited number of cases. That a physical or physiological execution of such an interminable series of operations is impossible is readily recognized by us; but we cannot or will not subject to the same limitations the power of our mind. Indeed, when our mind contemplates the future, it flees its mortal shell to find refuge within an infinite [Pg 134]being endowed with limitless memory and eternal life. To this immortal being the infinite past was once an infinite future; his inferences from past to future derive from an infinite experience; to him the infinite is not an article of faith but a phase of reality, since he knows no fear of oblivion.
Why should man endow himself with these divine attributes? What causes man to seek order and reason in the shifting chaos of sensations, and, by projecting himself into the future, perpetuate his life as it were? He who knows the answer to these questions holds the key to the mystery of reality.
Possessed by an ineffable will to permanence, man is urged onward in the faith that the future will resemble the past; that even as the present derives from the past, so is the future foreshadowed by the present; that the universe is governed by immutable laws; that his recurrent impressions can wrest from Nature the secret of these laws; that by willed acts he can foster these impressions and accelerate his knowledge of the universe; that no bound can ever be set to the reproduction of these willed acts; for what has been done or said once can ever be repeated.
This ineffable will to permanence may be the source of the two principles on which rest all science, pure and applied; of which the first sanctifies indefinite iteration [I], thus creating the exotic scheme of utmost generality and abstraction which we call mathematics; whilst the second sanctifies induction by inference, this cornerstone of empirical knowledge. If we reflect that the same will to permanence has ever been the source of religious revelation, we can but exclaim: "It is a strange world, this only world we know!"
Whatever is not thought is nil and void; because we can think only in terms of thought, and because all the words of which we dispose speak only thoughts; to say that there are things other than thoughts is a statement without meaning. And yet—strange contradiction to those who believe in time—geological history teaches that life is but a short episode between two eternities of death, and that within this very episode conscious thought did not and will not last but an instant. Thought: just a flash of lightning in the middle of a long night. And this flash is all!
Henri Poincaré, Science and Reality
ALL principles of relativity [R] declare that it is impossible for a terrestrial observer, or for any moving observer for that matter, to determine the absolute motion in which he may be engaged. Nor can he relegate this task to "inanimate" observers in his environment, such as his apparatus or instruments, inasmuch as those too participate in his motion. The principle of indeterminacy, on the other hand, declares that it is impossible for any material observer to obtain a complete set of specifications which would describe the state of affairs within an atom that he is observing, on the ground that the observer, as well as any equipment that he may wish to use for the purpose, are themselves aggregates of atoms.
Both principles unite in the declaration that is is impossible, by means of observations alone, to separate the observata [O] from the observer. That the individual idiosyncrasies of an observer may be discounted by comparing his results with those of others, is granted; but that the collective predilections, which are common to all observers, and which may be due either to their participation in one and the same motion, or to their atomic structures [Pg 136]may be so discounted, is denied, on the ground that any observation, however judiciously planned, is inevitably tinged with these collective peculiarities.
Yet, precisely this separation of the observata [O] from the observer has been the historical aim of science. In the past human experience was regarded as a sort of limpid fluid covered with a scum of impurities: to reach objective reality, it was, necessary to remove this scum of erroneous judgments. While the task was admittedly difficult, it was not considered beyond human powers, for, it was confidently believed that the progress of science tended in the direction of freeing experience from these subjective impurities, and of uncovering the residue which reflected the truly objective world.
That such an objective world actually existed, that it was entirely independent of man's emotions, or thoughts, or even of his very existence, was not subject to serious doubt. Here, the man of science and the man on the street were in nearly perfect agreement. Indeed, the objective world which consciousness imposes upon man is a perfect complement to his inner self. It possesses all the attributes which in him are conspicuous by their absence: it is absolute, infinite, and eternal, it is governed by permanences and certainties. In brief, it is all that man is not; and yet, paradoxically enough, it is rational, i.e., accessible to man's reason.
To attain through human experience the universe which is independent of human experience—such was the acknowledged goal of classical science; that was why it sought absolute time and space, absolute laws and constants. The whole history of classical science can be viewed as such a quest of the absolute. On reason was bestowed the function to lead in the quest, for, it was confidently believed that reason had the power to discount human foibles and dispel the shadows cast by our incoherent or conflicting sense-impressions.
The quest was arduous, the goal elusive. The center of the immobile space had to be constantly shifted, further and further into the infinite expanses of the apparent universe. The absolute instant, when duration had begun, was lost in the infinite stretches [Pg 137]of the past. After thousands of years of searching man was admittedly no nearer the goal than at the outset. It began to dawn upon him that the absolute [A] may be just a ballast which he, in the course of his long journey, had been forced to abandon bag by bag, that he might rise to higher peaks from which to survey his universe.
The last bags have been cast. The firm realities of space and time have been abandoned. The absolute and rigid web which was hitherto regarded as the theatre of all events has become a gigantic squirming four-dimensional mollusk merged with duration. The immutable succession of events, robbed of space and time, has lost its meaning. For, what significance can be ascribed to succession, when the very concepts of space and time, having become but perplexing confusions, must be withdrawn from scientific circulation.
Equally perplexing is the new picture of the microcosmos. An aggregate of atoms is observing an atom through another aggregate of atoms: the modern physicist has abandoned the belief of his predecessors that the observed atom is immune to the tremendous aggregates of similar atoms which are observing it. There is no escape from the uncertainty principle: [I] the "ultimate" constituent of matter, the electron, has lost position and speed; it has lost its very individuality.
The universe of discourse of classical physics was locked: the past dovetailed with the present, the present with the future; there was no room in it for true contingencies, and the apparent contingencies were explained by man's intellectual limitations. Because of these limitations man was compelled to deal in probabilities. Yet chance was a mere appearance, just a measure of human ignorance. Certainty was absolute, for, at any given instant the universe was a function of its past, the solution of a system of differential equations which admitted but one solution.
The universe was like a river: an absolute observer stood on shore and, watch in hand, observed its uniform flow. He stood behind a surveying instrument: his keen eyes could single out any particle of this flowing body, and register and plot its incessant peregrinations. Man was like a traveler on the river: he too had [Pg 138]been provided with surveying instruments and chronometer, he too could single out a particle of the fluid and watch its changes in space and time. Man's findings were not the same as those of the absolute observer, and he knew it. Moreover, he knew why and how they differed; he knew that his own findings were but appearances, and those of his absolute counterpart reality. Man could never hope to become absolute; yet he knew that he was the nearest thing to it, for, he had learned to discount his relative findings and adjust them to those of the absolute observer.
The advent of the new physical theories has profoundly modified this outlook.
Nowhere is a fixed shore to be found from which the fleeting and floating universe may be observed. The very quest of the absolute has been the pursuit of a mirage: it led man onward and upward, until it has brought him to the summit from where he can realize how fictitious has been his goal.
Gone is the picture of the universe as a rigid scaffolding at all joints of which keep ticking in perfect synchrony absolute clocks; gone is the conception of motion as a correspondence between space and time that could influence neither the structure of space nor the flow of time. The rigid scaffolding has turned out to be a flexible web; the moving particle is like a passing hurricane that sways and bends, and warps and strains the threads as the web recedes before it. The cosmic clocks have been degraded to the rank of local timepieces, each with a rhythm of its own when at rest, each furiously accelerating at the approach of a moving particle.
Changed, too, is the behavior of the particle! In classical days it was a lump of matter compelled to preserve during its peregrinations the quantity of matter it possessed and the energy it transported, unless it came into collision with another particle, in which case a redistribution of both energy and mass occurred, the sum total remaining unchanged. Today both concepts have lost significance. Neither mass nor energy are viewed as intrinsic properties of matter or of motion: both may sway and shift, and wax and wane.
[Pg 139]Certainty, too, has been declared an anthropomorphic delusion [I]. It grew out of the presence in man's environment of vast aggregates of matter. When one deals with large masses, the many contingencies attending a phenomenon are neutralized by their opposites, so that the prevalent appears as the necessary. But when we pass from matter in bulk to an atom, the conception looms as a fallacy. Atomic analysis raises chance [C] to the function of supreme law of nature; it reduces causation to a mere approximation to the law.
Classical science assigned to man an exceptional position in the scheme of things: he was capable of detaching himself from the ties that had chained him to the universal mechanism and appraise this latter in true perspective. To be sure, his consciousness too was but a link in the endless chain of cause and effect, yet the evolution of this consciousness was believed to be in the direction of greater freedom. His body was chained, but his mind was free to contemplate these chains, to classify, measure, and weigh them. The book of nature lay open before his eyes; he had but to decipher the code in which it was written, and his faculties were equal to the task.
This code was rational: the immutable order that was man's to contemplate was governed by rational laws; the universe had been designed on patterns which human reason would have devised, had it been entrusted with the task, the structure of the universe was reducible to a rational discipline; its code of laws could be deduced from a finite body of premises by means of the syllogisms of formal logic. These premises derived their validity not from speculation but from experience [E], which alone could decide the merit of a theory. Like Antaeus, who, harassed by Hercules, would restore his waning strength every time his body touched his mother Earth, so did theory constantly gain by contact with the firm reality of experience.
The mathematical method reflected the universe. It had the power to produce an inexhaustible variety of rational forms. Among these was that cosmic form which some day might embrace the universe in a single sweep. By successive approximations [Pg 140]science would eventually attain this cosmic form, for, with each successive step it was getting nearer to it. The very structure of mathematics guaranteed this asymptotic approach; for every successive generalization contained a larger portion of the universe, without ever abandoning any of the previously acquired territory.
Mathematics and experiment reign more firmly than ever over the new physics, but an all-pervading skepticism has affected their validity. Mathematics would collapse like a house of cards but for the belief that man may safely proceed as though he possessed a limitless memory, and an inexhaustible life lay ahead of him. It is on this belief that the validity of infinite processes is based, and these processes dominate mathematical analysis. But this is not all: arithmetic itself would lose its generality were the infinite refuted, for, our concept of whole number is inseparable from it; and so would geometry and mechanics. This catastrophe would, in turn, uproot the whole edifice of the physical sciences.
As to the validity of experience, it rests on our faith that the future will resemble the past. We believe that because in a series of events which appear to us similar in character a certain tendency has manifested itself, this tendency reveals permanence, and that this permanence will be the more assured for the future the more uniformly and regularly it has been witnessed in the past. And yet this validity of inference, on which all empirical knowledge [E] is based, may rest on no firmer foundation than human longing for certainty and permanence.
And this unbridgeable chasm between our unorganized experience and systematic experiment! Our instruments of detection and measurement, which we have been trained to regard as refined extension to our senses, are they not like loaded dice, charged as they are with preconceived notions concerning the very things which we are seeking to determine? Is not our scientific knowledge a colossal, even though unconscious, attempt to counterfeit by number the vague and elusive world perceived by our senses? Color, sound, and warmth reduced to frequencies [Pg 141]of vibrations, taste and odor to numerical subscripts in chemical formulae, is this the reality that haunts our consciousness?
Our minds have the capacity of conceiving allegorical worlds [P] and people these worlds with allegorical beings, endowed with consciousness, mobility and intelligence, who in the course of time could develop a cosmology, even as we did.
Seeking permanence and order in the complex of their conflicting perceptions, they would eventually discover in their environment objects which remain sensibly fixed in form and magnitude, turn these objects into rigid templets and standards, and proceed to measure and survey with their aid the world which surrounds them. Interpreting their free mobility as nonresistance on the part of the medium in which they move, they would conceive it homogeneous and isotropic, and believing, as we do, that no limit can be set to their mobility they would be led to view their medium as infinite. Their search for permanence would cause them to endow the theater of their activity with neutrality to expansion and contraction. Thus, in their quest of a rational interpretation of their spatial experience, they could develop a geometry formally equivalent to ours, and this no matter how fantastic their environment and conduct might appear to us.
But we need not stop here. Singling out some cyclic phenomena which recur in relative synchrony with their physiological processes, these beings could correlate these temporal series with their stream of consciousness. Regarding the laws of their cosmos as independent of their thinking, they would become convinced of the objective character of their time concept, and proceeding beyond the narrow confines of their experience, they would extend their findings to the world at large, conceiving their cosmos as floating with absolute uniformity on the stream of duration.
Having thus transferred to their cosmos their own predilections, they would arm their space with bristling forces and shackle their history to a causal chain. Yet, their minds suggesting other possible worlds, they would seek to establish the absolute character of their own; and failing in this quest, they would be led to suspect that their cosmology was tinged with a collective bias. [Pg 142]Thus, awakening one day to the stark realization that nowhere in their universe can the assurance be found that they had not been the victims of a cruel hoax, they would plunge into a profound skepticism which would shake the foundation of their knowledge.
Mathematics holds no nostrum for skepticism. Mathematics is but a storeroom of conceptual patterns. The verdict is an alternative: either fit experience into one of these patterns, or declare experience irrational. If experience is irrational, then there can be no science; and if experience is rational, then it must conform to one of these conceptual schemes. It is the problem of any science to find a conceptual pattern for the particular aspect of experience with which it deals. Alas! These patterns are like so many Procrustean beds, some too long, some too short. The schemes were not made to fit experience, so experience must be stretched or amputated, as the case may require, to fit one of the schemes.
But does not the history of geometry suggest some freedom of choice, inasmuch as an intuitive notion may be flexible enough to fit more than one conceptual pattern? Yes, indeed! But this choice was proffered too late: the evolution of the race had decided the issues long before man knew that he had a choice; the postulates back of scientific speculation had finished by penetrating into the very fabric of man's mind, until they had lost their character of hypotheses and came to be construed by him as indispensable to thought.
After centuries of futile endeavor man had to concede that these postulates were not logical necessities. He then pinned his hope on experience. Experience, he thought, would confirm that the ambitious structure erected on these axioms floats not on the uncharted and unchartable ocean of uncertainties, but rests on the rock of the Absolute [A]. There was a time—and it was not so long ago—when any doubts cast on this faith in experience were silenced by proud affirmatives. Between Man and Truth stood only the foibles of the individual; it was the function of experimental science to eliminate this individual bias, or discount it; [Pg 143]it was the credo of the scientist that the collective effort of his group could achieve this gigantic task.
Today, Science has disavowed this proud position. Today, the bias of the individual has paled into insignificance before the collective bias of the race, which can neither be measured nor even detected. Invisible and intangible, this phantom bars the road to all absolute knowledge, and casts doubt on all verities but one: man is the measure of all things, and there is no other measure.
I contemplate the silhouetted skyline of the city: flat surfaces and straight edges, relieved by an occasional peak or round cupola. I think of the landscape beyond: the jagged hills, the ruffled rivers, the unruly outlines of woods and clearings. The work of man etched against the capricious background of Nature!
I watch the smoothly flowing traffic, I sense the rhythmic motions of valve and gear; and I think of quake and flood, of flame, avalanche and tempest. Man's ordered life against the sporadic convulsions of Nature!
I scan the interpretations which Science has offered to explain the world to man, the thoughts and schemes by which man has planned to capture and hold recalcitrant Nature. Here, too, the flat, the straight, the smooth and the steady [S] reign undisputed. They guide man's quest for harmony and order, they rule the laws which he has read into Nature, they rule the very instruments designed to vindicate these laws.
Wherever man could, he put these concepts in command, and whenever he could not do it without violating the evidence of his senses, he invoked the Infinite to reduce the intricate forms of his perceptions to these elementary notions. The flat, the straight, the steady and the smooth! Wherever man passed, he left these imprints on the sands of time.
I think of Plato [P] to whom these concepts were the incorporeal and immortal thoughts of a Creator; of D'Alembert's [D] suspicions that they were but abuse of speech; of Kant [K] who viewed them as judgments prior to all experience; of Hume [H] to whom they were but latent reflections of cumulative experience; of Poincaré who [Pg 144]regarded them as sheer conventions, sanctified by tradition and convenience, but which, without contradicting either logic or experience, could by collective agreement be replaced by other conventions.
In the guise of axioms, postulates, hypotheses or attributes, these concepts have studded the battleground on which opposing philosophical schools have met and fought: realists, materialists, positivists, empiricists, nominalists, conventionalists, solipsists, and those who sought to sum up all human knowledge in the two short words: as if. The battle of ideas goes on, the ideas remain as elusive as ever.
Were these concepts implanted in man with the first spark of consciousness? Are they but the outgrowth of the age-old conflict aimed at reconciling man's mobility with the static impressions of man's senses? Or are these concepts just symbols of human perplexity, and Science but an organized effort to impose this perplexity on Nature?
Ignoramus et ignorabimus!
Jules Henri Poincaré was born in Nancy on April 29, 1854, and died in Paris on July 16, 1912. The pertinent events of his life are covered in the first chapter of this work. For a detailed biography as well as an analysis of his scientific work by Gaston Darboux, the reader is referred to Volume II of Poincaré's Collected Works.
Poincaré's memoirs on mathematics, and his treatises on mathematical physics and celestial mechanics lie outside the ken of non-mathematicians. They are also outside the scope of the present book which is concerned only with the scientific philosophy of Poincaré.
His views on the foundations of science were gathered in four volumes, the last of which appeared posthumously. They are:
La Science et l'Hypothèse,
Science et Méthode,
La Valeur de la Science,
Dernières Pensées.
Action at a Distance 75
Algebra 106
Analysis, Mathematical 120
Arithmetic 128
Beltrami 46
Berkeley, Bishop 112
Bertrand, J. 10
Bolyai 46
Cantor-Dedekind Axiom 125
Centrifugal Force 101
Clock 63-68
Conservation 23
Continuum 125-128
Copernicus 84
Cosmic Time 72
Curvature 95
Descartes 84
Determinism 26
Distance 78
Diurnal Motion 67
Encyclopedists 15
Equilibrium 69
Equivalent, Mechanical 22
Existence 38
Experience 52
Fermat 24
Geometry, Descriptive 2
Geometry, Euclidean 28, 33, 77, 80, 81
Geometry, Non-Euclidean 4, 28, 45-49
Goethe 112
Hamilton 24
Heliocentric Hypothesis 30
Homunculus 115
Induction, Mathematical 129-132
Inductive Inference 131-132
Industrial Revolution 14, 17-19
Infinity 76, 120, 121-125, 129-134
Kant 143
Kinematics 82
Klein 4
Light 77-81
Limit 123
Mathematics 105-112
Maupertuis 24
Measurement 118-120
Memory 61
Michelson 99
Mobility 41
Morley 99
Napoleon 13
Neutrality 75
Newcomb 24
Newton 5, 22, 31, 32, 67, 83, 87, 95, 100
Nietzsche 112
Operational 77
Oscar II, King of Sweden 5
Painlevé 9
Pendulum 65
Periodic Phenomena 62-65
Physics 109-112
Poincaré, Family 1
Poincaré, Henri; Biography, 1-13
Poincaré, Raymond 1
Precedence 72
Pseudo-plane 46
Pythagoras 21
Reaction 89
Real number 124
Reality, Objective 12, 60, 72, 91, 113
Rectilinear 75
Refraction 58
Relativity 7, 33-36, 43, 72-75, 87-92, 95-104, 135
Rhythm 61
Rigidity 38, 40, 48-51, 52-60, 64, 91
Russell 131
Saccheri 45
Self-congruence 48-51
Sidereal Day 64
Signal 74-80
Solar Day 64
Solipsism 12
Sound 75
Speculation, Religious 121
Speculation, Scientific 105-107
Sphere 46
Stability 6
Stress 94
Sublimation 115-117
Sufficient Reason 66
Synthetic Judgment 44
Temperature 83
Thales 39
Three-body Problem 5, 6, 7, 97
Tides 7
Transfinite 122
Transitivity 117
Uniform 55, 61, 64, 75, 78, 84, 91
Velocity 81
Volume 92
Wallis 37
Zenith 64